题目内容
7.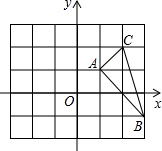 如图,在直角平面坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,-1)、C(2,2).
如图,在直角平面坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,-1)、C(2,2).(1)作出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC沿A点顺时针旋转90°,求点B经过的路径长.
分析 (1)利用关于y轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点得到△A1B1C1;
(2)利用网格特点和旋转的性质画出△ABC沿A点顺时针旋转90°所得的△AB2C2,然后根据弧长公式计算点B经过的路径长.
解答 解:(1)如图,△A1B1C1为所作;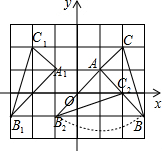
(2)AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
点B经过的路径长=$\frac{90•π•2\sqrt{2}}{180}$=$\sqrt{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
12.菱形ABCD的一条对角线的长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
| A. | 16 | B. | 12 | C. | 12或16 | D. | 无法确定 |
17.下列说法正确的是( )
| A. | 等角的补角相等 | B. | 相等的角是对顶角 | ||
| C. | 和为180°的两角互余 | D. | 内错角互补,两直线平行 |
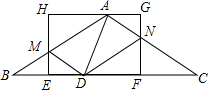 如图,在等腰三角形ABC中,AB=AC,点D是BC边上一点,BD<CD,点E是BD的中点,矩形EFGH的边EF在BC上,CF=AH,GH经过点A,AB、AC分别交HE、GF于点M、N.
如图,在等腰三角形ABC中,AB=AC,点D是BC边上一点,BD<CD,点E是BD的中点,矩形EFGH的边EF在BC上,CF=AH,GH经过点A,AB、AC分别交HE、GF于点M、N. 如图,矩形ABCD中,BC边所在直线上有E、F两点,且BE=CF,请用无刻度的直尺画出该图的对称轴.
如图,矩形ABCD中,BC边所在直线上有E、F两点,且BE=CF,请用无刻度的直尺画出该图的对称轴. 如图,在正方形ABCD中,边长为2的等边△AEF的顶点E、F分别在BC和CD上,下列结论:
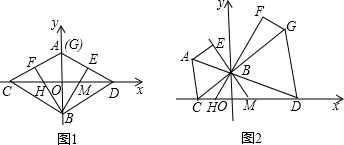
如图,在正方形ABCD中,边长为2的等边△AEF的顶点E、F分别在BC和CD上,下列结论: 已知:如图,平面直角坐标系中有一个等腰梯形ABCD,且AD∥BC,AB=CD,点A在y轴正半轴上,点B、C在x轴上(点B在点C的左侧),点D在第一象限,AD=3,BC=11,梯形的高为2,双曲线y=$\frac{m}{x}$经过点D,直线y=kx+b经过A、B两点.
已知:如图,平面直角坐标系中有一个等腰梯形ABCD,且AD∥BC,AB=CD,点A在y轴正半轴上,点B、C在x轴上(点B在点C的左侧),点D在第一象限,AD=3,BC=11,梯形的高为2,双曲线y=$\frac{m}{x}$经过点D,直线y=kx+b经过A、B两点.