题目内容
6.解不等式组:$\left\{\begin{array}{l}{1-\frac{x+1}{3}≥0}\\{3+4(x-1)>1}\end{array}\right.$,并把解集表示在数轴上.分析 先对不等式组进行化简,然后在数轴上分别画出x的取值,它们的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{1-\frac{x+1}{3}≥0①}\\{3+4(x-1)>1②}\end{array}\right.$
由①得x≤2,
由②得x>$\frac{1}{2}$,
不等式组的解集为$\frac{1}{2}$<x≤2,
不等式得解集在数轴上表示为
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.要注意x是否取得到,若取得到则x在该点是实心的.反之x在该点是空心的.

练习册系列答案
相关题目
14.在实数0、-1、$\sqrt{2}$、0.12345中,无理数的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
18.分式方程$\frac{2}{x-3}=\frac{3}{x}$的解是( )
| A. | x=-9 | B. | x=9 | C. | x=3 | D. | $x=\frac{9}{5}$ |
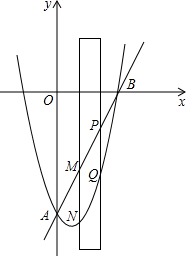 如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).
如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).