题目内容
16.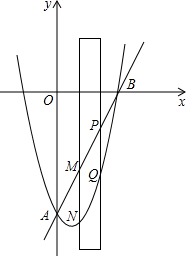 如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).
如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).(1)抛物线的函数关系式为y=x2-2x-8;
(2)有一宽度为1的直尺平行于y轴,在点A、B之间移动,直尺两长边所在直线被线段AB和抛物线截得两线段MN(M在N上方)、PQ(P在Q上方),设M点的横坐标为m,(0<m<3)
①若连接MQ,求以M、P、Q为顶点的三角形和△AOB相似时,m的值;
②若连接NQ,请直接写出m为何值时,四边形MNQP的面积最大.
分析 (1)将点A和点B的坐标代入抛物线的解析式可求得b、c的值,于是可得到抛物线的解析式;
(2)如图1所示:连接MQ.先求得直线AB的解析式,当△AOB∽△PQM时.可知MQ∥OB,设点M的坐标为(m,2m-8),则点Q的坐标为(m+1,m2-9)然后由M和Q的纵坐标相等可得到m的值;②当△PMQ∽△AOB时,过点M作MN⊥PQ,然后证明△MNQ∽△AOB,由相似三角形的性质可得到NQ=$\frac{1}{2}$,设点M的坐标为(m,2m-8),则点Q的坐标为(m,m2-9),然后根据NQ的长列方程求解即可;
(3)设点M的坐标为(m,2m-8),则点N(m,m2-2m-8)、P(m+1,2m-6),Q(m,m2-9),然后由四边形MNQP的面积=$\frac{1}{2}$×1×(MN+PQ)得到四边形MNQP的面积与m的函数关系式,从而可求得m的值.
解答 解:(1)∵抛物线y=x2+bx+c交y轴于点A(0,-8),
∴c=-8.
∵将B(4,0)代入y=x2+bx-8得:16+4b-8=0,解得:b=-2.
∴抛物线的解析式为y=x2-2x-8.
故答案为:y=x2-2x-8.
(2)如图1所示:连接MQ.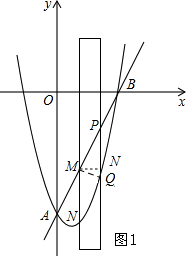
设AB的解析式为y=kx+b.
将点A和点B的坐标代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=-8}\end{array}\right.$,
解得:k=2,b=-8.
∴直线AB的解析式为y=2x-8.
∵PQ∥OA,
∴∠MPQ=∠OAB.
i.当△AOB∽△PQM时.则∠AOB=∠PQM=90°.
∴MQ∥OB.
设点M的坐标为(m,2m-8),则点Q的坐标为(m+1,m2-9).
∵MQ∥OB,
∴2m-8=m2-9,解得m=$\sqrt{2}$+1或m=-$\sqrt{2}$+1(舍去).
∴当m=$\sqrt{2}$+1时,△AOB∽△PQM.
ii.当△PMQ∽△AOB时,如图1所示:过点M作MN⊥PQ.
∵△PMQ∽△AOB,
∴∠PMQ=∠AOB=90°,∠PQM=∠ABO.
∴∠MQN=∠ABO.
∵MN⊥PQ,
∴∠MNQ=90°.
∴∠MNQ=∠AOB.
∴△MNQ∽△AOB.
∴$\frac{QN}{MN}=\frac{OB}{OA}$=$\frac{1}{2}$.
∵MN=1,
∴NQ=$\frac{1}{2}$.
设点M的坐标为(m,2m-8),则点Q的坐标为(m,m2-9).
∴NQ=-m2+2m+1.
∴-m2+2m+1=$\frac{1}{2}$.
解得:m=$\frac{\sqrt{6}}{2}$+1或m=-$\frac{\sqrt{6}}{2}$+1(舍去).
综上所述,m的值为$\sqrt{2}$+1或$\frac{\sqrt{6}}{2}$+1.
②设点M的坐标为(m,2m-8),则点N(m,m2-2m-8)、P(m+1,2m-6),Q(m,m2-9).
四边形MNQP的面积=$\frac{1}{2}$×1×(MN+PQ)=$\frac{1}{2}$(-2m2+6m+3)=-m2+3m+$\frac{3}{2}$.
当m=$\frac{-3}{-1×2}$=$\frac{3}{2}$时,四边形MNQP的面积有最大值.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、相似三角形的性质和判定、二次函数的图象和性质得到关于m的方程以及四边形MNQP的面积与m的函数关系式是解题的关键.

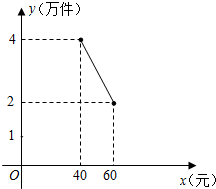 为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示. 已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).
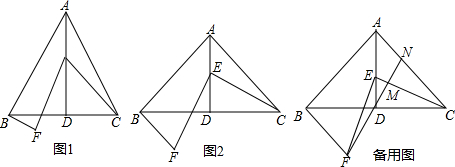
已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).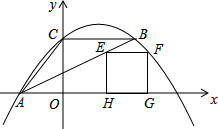 如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.
如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.