题目内容
9.已知BD是△ABC的角平分线,DE∥BC,交AB于点E.(1)如图1,求证:△BED是等腰三角形;
(2)当时,如图2,在线段BC上取一点F,使四边形BFDE是菱形,连接EF,在不添加任何辅助线的情况下,请写出与△BEF面积一定相等的所有三角形(不包括△BEF本身).

分析 (1)由角平分线的定义得出∠ABD=∠DBC,再由平行线的性质得出∠DBC=∠BDE,证出∠ABD=∠BDE,根据等角对等边即可得出结论;
(2)由菱形的性质得出OB=OD=OE=OF,EF⊥BD,得出△OBE的面积=△OBF的面积=△ODF的面积=△ODE的面积,得出△BEF的面积=△BED的面积=△BFD的面积=△EFD的面积.
解答 (1)证明:∵BD是∠ABC的平分线,
∴∠ABD=∠DBC,
∵DE∥BC,
∴∠DBC=∠BDE,
∴∠ABD=∠BDE,
∴BE=DE
即△BED是等腰三角形;
(2)解:与△BEF面积相等的所有三角形分别是△BED、△BFD、△EFD;理由如下:如图所示: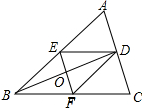 ∵四边形BFDE是菱形,
∵四边形BFDE是菱形,
∴OB=OD=OE=OF,EF⊥BD,
∴△OBE的面积=△OBF的面积=△ODF的面积=△ODE的面积,
∴△BEF的面积=△BED的面积=△BFD的面积=△EFD的面积.
点评 本题考查了菱形的性质、等腰三角形的判定、平行线的性质;熟练掌握菱形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
19.已知(a-3)x|a|-2+6=0是关于x的一元一次方程,则a的值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 0 |
18.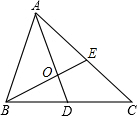 如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )
如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )
 如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )
如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )| A. | 8 | B. | 4$\sqrt{10}$ | C. | 12 | D. | 14 |
 按要求用尺规作图并填空(保留作图痕迹):
按要求用尺规作图并填空(保留作图痕迹):