题目内容
18.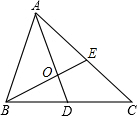 如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )
如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )| A. | 8 | B. | 4$\sqrt{10}$ | C. | 12 | D. | 14 |
分析 首先根据重心到顶点的距离与重心到对边中点的距离之比为2:1,求出AO、OE的长度各是多少;然后在直角三角形AOE中,根据勾股定理,求出AE的长度;最后根据AD⊥BE用AE的长度乘以2,求出AC的值为多少即可.
解答 解:∵O是△ABC的重心,
∴OE=$\frac{1}{1+2}×6$
=$\frac{1}{3}×6$
=2
∵AD⊥BE,
∴$AE=\sqrt{{6}^{2}{+2}^{2}}=2\sqrt{10}$,
∵E是AC的中点,
∴AC=2AE=2×2$\sqrt{10}=4\sqrt{10}$.
故选:B.
点评 (1)此题主要考查了三角形的重心的判断和性质的应用,要熟练掌握,解答此题的关键是要明确:重心到顶点的距离与重心到对边中点的距离之比为2:1.
(2)此题还考查了直角三角形的三边的关系,以及勾股定理的应用,要熟练掌握.

练习册系列答案
相关题目

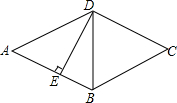 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,AE:DE=4:3,则下列结论中正确的个数为( )
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,AE:DE=4:3,则下列结论中正确的个数为( )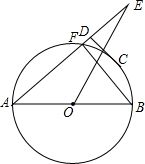 如图,⊙O的直径AB=8,点E在圆外,AE交⊙O于点F,C是圆心上一点,CD⊥AE于点D,AF=2CD=4$\sqrt{2}$.
如图,⊙O的直径AB=8,点E在圆外,AE交⊙O于点F,C是圆心上一点,CD⊥AE于点D,AF=2CD=4$\sqrt{2}$.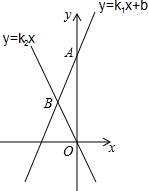 如图,一次函数y=k1x+b的图象与y轴交于点A(0,10),与正比例函数y=k2x的图象交于第二象限内的点B,且△AOB的面积为15,AB=BO,求正比例函数与一次函数表达式.
如图,一次函数y=k1x+b的图象与y轴交于点A(0,10),与正比例函数y=k2x的图象交于第二象限内的点B,且△AOB的面积为15,AB=BO,求正比例函数与一次函数表达式. 如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=$\frac{1}{2}$AB,点E、F分别为AB、AD的中点,求△AEF与多边形BCDFE的面积之比.
如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=$\frac{1}{2}$AB,点E、F分别为AB、AD的中点,求△AEF与多边形BCDFE的面积之比.