题目内容
19．算式22011×32×5×7，得数的个位数字是0．分析 先找出2的乘方的尾数的特征，再找出3的平方位数的特征，从而得出22011与32的尾数，再把它们与5，7相乘即可解答．
解答 解：2n的末位数字按2，4，8，6的顺序循环，而32的末位数字是9，
因为2011是4k+3形状的数，
所以22011的末位数字是8，
8×9×5×7=2520，
所以22011×32×5×7的个位数字是0．
故答案为：0．
点评 本题主要考查尾数的特征，熟练找出2与3的乘方的尾数是解答本题的关键．
练习册系列答案
相关题目
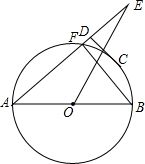如图，⊙O的直径AB=8，点E在圆外，AE交⊙O于点F，C是圆心上一点，CD⊥AE于点D，AF=2CD=4$\sqrt{2}$．
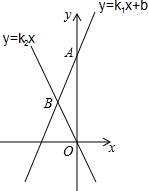如图，一次函数y=k1x+b的图象与y轴交于点A（0，10），与正比例函数y=k2x的图象交于第二象限内的点B，且△AOB的面积为15，AB=BO，求正比例函数与一次函数表达式．
如图所示，在△ABC中，O为∠ABC，∠ACB的平分线的交点，如果OD⊥AB，OE⊥AC，OF⊥BC，垂足分别为D，E，F，OD与OE是否相等？为什么？
如果一等腰三角形的底边与腰的比等于黄金比，那么这个等腰三角形就叫做黄金三角形，请你以图中的线段AB为腰，用直尺和圆规，作一个黄金三角形ABC．
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD，CD=$\frac{1}{2}$AB，点E、F分别为AB、AD的中点，求△AEF与多边形BCDFE的面积之比．