题目内容
2. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出的以下四个结论,(1)abc=0,(2)a+b+c>0,(3)a>b,(4)a-b+c>0其中正确的是(1)(4)(填序号).
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出的以下四个结论,(1)abc=0,(2)a+b+c>0,(3)a>b,(4)a-b+c>0其中正确的是(1)(4)(填序号).
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答  解:(1)如图所示,抛物线经过原点,则c=0,故abc=0,故正确;
解:(1)如图所示,抛物线经过原点,则c=0,故abc=0,故正确;
(2)如图所示,当x=1时,y<0,即a+b+c>0,故错误;
(3)如图所示,抛物线开口方向向下,则a<0,
又抛物线对称轴位于y轴的右侧,则a、b异号,即b>0,
所以a<b,
故错误;
(4)如图所示,当x=-1时,y>0,即a-b+c>0,故正确;
综上所述,正确的结论是(1)(4).
故答案是:(1)(4).
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.某班50名同学的数学成绩为:5人100分,30人90分,10人75分,5人60分,则这组数据的众数和平均数分别是( )
| A. | 90,85 | B. | 30,85 | C. | 30,90 | D. | 90,82 |
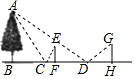 某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).
某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸). 在如图中填入适当的数,使得横向、纵向的分数之和为1,那么A格内填$\frac{11}{32}$.
在如图中填入适当的数,使得横向、纵向的分数之和为1,那么A格内填$\frac{11}{32}$.