题目内容
9. 如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:
如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:①a<0,②b<0,③b2-4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①② |
分析 ①由抛物线开口向下即可得出a<0,①成立;②由抛物的对称轴x=-$\frac{b}{2a}$>0结合a<0即可得出b>0,②不成立;③由抛物线与x轴有两个交点即可得出b2-4ac>0,③成立;④由抛物线的对称性可得出AE=BE,结合点B的坐标以及OE=CD即可得出AE+CD=4,④成立.综上即可得出结论.
解答 解:①∵抛物线开口向下,
∴a<0,①成立;
②∵抛物线的对称轴为x=-$\frac{b}{2a}$>0,
∴b>0,②不成立;
③∵抛物线与x轴有两个交点,
∴b2-4ac>0,③成立;
④∵DE为抛物线的对称轴,
∴AE=BE.
∵B点坐标为(4,0),
∴OB=OE+BE=CD+AE=4,④成立.
故选C.
点评 本题考查了抛物线与x轴的交点以及二次函数图象与系数的关系,结合二次函数图象逐一分析四条结论是否成立是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
19.“五•一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
14.某农场开挖一条长480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么求x时所列方程正确的是( )
| A. | $\frac{480}{x-4}$-$\frac{480}{x}$=4 | B. | $\frac{480}{x}$-$\frac{480}{x+4}$=20 | C. | $\frac{480}{x-20}$-$\frac{480}{x}$=4 | D. | $\frac{480}{x}$-$\frac{480}{x+20}$=4 |
1.抛物线y=2(x+3)2-2的顶点坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
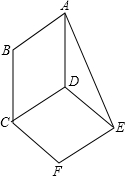 如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠DAE=25°,则∠F的度数为110°.
如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠DAE=25°,则∠F的度数为110°.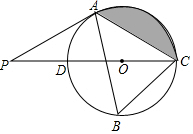 如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.
如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.
 (1)试帮助考古人员“修补”这个破碎的圆盘(保留作图痕迹,并写出作法)
(1)试帮助考古人员“修补”这个破碎的圆盘(保留作图痕迹,并写出作法)