题目内容
8.直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为3.5.分析 首先根据勾股定理求得该直角三角形的斜边是5,再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算.
解答 解:∵直角三角形两直角边为3,4,
∴斜边长=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴外接圆半径=$\frac{5}{2}$=2.5,内切圆半径=$\frac{3+4-5}{2}$=1,
∴外接圆和内切圆半径之和=2.5+1=3.5.
故答案为:3.5.
点评 本题考查的是三角形的内切圆与内心,此题要熟记直角三角形外接圆的半径和内切圆的半径公式:外接圆的半径等于斜边的一半;内切圆的半径等于两条直角边的和与斜边的差的一半.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.“五•一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.使代数式$\frac{2x}{x-2}$有意义的x的取值范围为( )
| A. | x>2 | B. | x≠0 | C. | x<2 | D. | x≠2 |
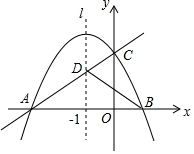 如图,已知抛物线y=ax2+bx+c(a<0,c>0)与x轴交于A,B两点,与y轴交于点C,其对称轴l为x=-1,直线y=kx+m经过A,C两点,与抛物线的对称轴l交于点D,且AD=2CD,连接BC,BD.
如图,已知抛物线y=ax2+bx+c(a<0,c>0)与x轴交于A,B两点,与y轴交于点C,其对称轴l为x=-1,直线y=kx+m经过A,C两点,与抛物线的对称轴l交于点D,且AD=2CD,连接BC,BD.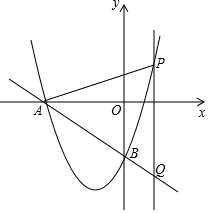 如图,已知直线l:y=-$\frac{3}{4}$x-3与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c经过A、B两点,且对称轴为直线x=-$\frac{3}{2}$.
如图,已知直线l:y=-$\frac{3}{4}$x-3与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c经过A、B两点,且对称轴为直线x=-$\frac{3}{2}$.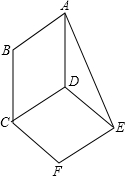 如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠DAE=25°,则∠F的度数为110°.
如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠DAE=25°,则∠F的度数为110°.