题目内容
 如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3
| 5 |
考点:切线的性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)根据等腰三角形的性质,可得∠ACO与∠CAO的关系,根据平行线的性质,可得∠DAC与∠ACO的关系,根据等量代换,可得答案;
(2)根据勾股定理,可得AD的长,根据等腰三角形的性质,可得AE与AC的关系,根据相似三角形的判定与性质,可得答案.
(2)根据勾股定理,可得AD的长,根据等腰三角形的性质,可得AE与AC的关系,根据相似三角形的判定与性质,可得答案.
解答:(1)证明:连结OC,
∵OA=OC,
∴∠ACO=∠CAO (等腰三角形,两底角相等)
∵CD切⊙O于C,
∴CO⊥CD,
又∵AD⊥CD
∴AD∥CO
∴∠DAC=∠ACO (两直线平行,内错角相等)
∴∠DAC=∠CAO(等量代换)
∴AC平分∠BAD;
(2)过点E画OE⊥AC于E,
在Rt△ADC中,AD=
=6
∵OE⊥AC,∴AE=
AC=
∵∠CAO=∠DAC,∠AEO=∠ADC=Rt∠
∴△AEO∽△ADC
∴
=
即
=
∴AO=
即⊙O的半径为
.

∵OA=OC,
∴∠ACO=∠CAO (等腰三角形,两底角相等)
∵CD切⊙O于C,
∴CO⊥CD,
又∵AD⊥CD
∴AD∥CO
∴∠DAC=∠ACO (两直线平行,内错角相等)
∴∠DAC=∠CAO(等量代换)
∴AC平分∠BAD;
(2)过点E画OE⊥AC于E,

在Rt△ADC中,AD=
(3
|
∵OE⊥AC,∴AE=
| 1 |
| 2 |
3
| ||
| 2 |
∵∠CAO=∠DAC,∠AEO=∠ADC=Rt∠
∴△AEO∽△ADC
∴
| AE |
| AD |
| AO |
| AC |
即
| ||||
| 6 |
| AO | ||
3
|
∴AO=
| 15 |
| 4 |
即⊙O的半径为
| 15 |
| 4 |
点评:本题考查了切线的性质,(1)利用了切线的性质,等腰三角形的性质,平行线的性质;(2)利用了勾股定理,等腰三角形的性质,相似三角形的判定与性质.

练习册系列答案
相关题目
下列运算正确的是( )
| A、-x2•x3=-x6 | ||
| B、(a-b)2=a2-2ab+b2 | ||
| C、(a2+b2)2=a4+b4 | ||
D、
|
 在△ABC中,AD⊥BC,BC的垂直平分线交AC于E,BE交AD于F.求证:E在AF的垂直平分线上.
在△ABC中,AD⊥BC,BC的垂直平分线交AC于E,BE交AD于F.求证:E在AF的垂直平分线上.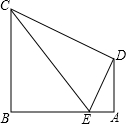 如图,四边形ABCD中,AD⊥AB,BC⊥AB,BC=2AD,DE⊥CD交边AB于E,连接CE,若△CDE与四边形ABCD的面积之比为2:5,则cos∠BCE的值为
如图,四边形ABCD中,AD⊥AB,BC⊥AB,BC=2AD,DE⊥CD交边AB于E,连接CE,若△CDE与四边形ABCD的面积之比为2:5,则cos∠BCE的值为