题目内容
8.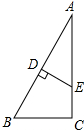 如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.
如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D,E.(1)求证:AE=2CE;
(2)求证:DE=EC.
分析 (1)首先连接BE,由在△ABC中,∠C=90°,∠A=30°,可求得∠ABC的度数,又由AB的垂直平分线交AB于点D,交AC于点E,根据线段垂直平分线的性质,可得AE=BE,继而可求得∠CBE的度数,然后由含30°角的直角三角形的性质,证得AE=2CE;
(2)通过BE=AE,得到∠ABE=∠A=30°,求得∠CBE=∠ABE=30°,根据角平分线的性质即可得到结论.
解答  解:(1)连接BE,
解:(1)连接BE,
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE;
(2)∵BE=2CE,AE=2CE;
∴BE=AE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABE=30°,
∵DE⊥AB,∠C=90°,
∴DE=CE.
点评 此题考查了线段垂直平分线的性质、直角三角形的性质、等腰三角形的性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
16.下列多项式乘法中不能用平方差公式计算的是( )
| A. | (2x2y-1)(-2x2-1) | B. | (a3-b3)(b3-a3) | C. | (a+b)(a-b) | D. | (a2+b2)(b2-a2) |
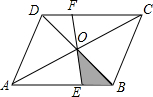 如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.
如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.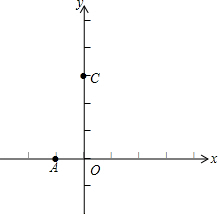 在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.
在平面直角坐标系xOy(如图)中,经过点A(-1,0)的抛物线y=-x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称.
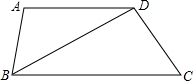 如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.
如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.