题目内容
16.解不等式组$\left\{\begin{array}{l}{2-x>0}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}\end{array}\right.$把它的解集在数轴上表示出来,并求该不等式组所有整数解的和.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,将解集表示在数轴上,再把所有整数解相加可得.
解答 解:解不等式2-x>0,得:x<2,
解不等式$\frac{5x+1}{2}+1≥\frac{2x-1}{3}$,得:x≥-1,
故不等式组的解集为:-1≤x<2,
将不等式组解集表示在数轴上如下:
所有整数解的和为:-1+0+1=0.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
6.已知a,b,c是三角形的三条边,则|a+b-c|-|c-a-b|的化简结果为( )
| A. | 0 | B. | 2a+2b | C. | 2c | D. | 2a+2b-2c |
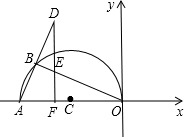 在平面直角坐标系中,点A(-5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=$\frac{3}{2}$或6.
在平面直角坐标系中,点A(-5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=$\frac{3}{2}$或6.