��Ŀ����
15����ͼ1����֪��ABC�У�AB=AC����BAC�Ķ���Ϊ������D�ǵױ�BC��һ���㣬����ABD�Ƶ�A��ʱ����ת���ȵõ���ACE������DE����1����֤����ABC�ס�ADE��
��2����ͼ2������D�˶���BC�е�ʱ������E��EF��BC��AC�ڵ�F������DF���ж��ı���CDFE����״��������֤����
��3���ڣ�2���������£���ABC����������BAC=90��ʱ���ı���CDFEΪ�����Σ�

���� ��1��������ת�����ʿɵ�AB=AC��AD=AE����BAD=��CAE���Ӷ��ɵ�$\frac{AB}{AD}$=$\frac{AC}{AE}$����BAC=��DAE�����ɵõ���ABC�ס�ADE��
��2����֤��ACE=��ABD=��ACD=��EFC������EF=EC���Ӷ��ɵ�EF=EC=BD=DC���ɴ˿�֤���ı���CDFE�����Σ�
��3��Ҫʹ����CDFE�������Σ�ֻ���DCE=90�㣬ֻ���DCF=45�㣬ֻ���BAC=90�㣮
��� �⣺��1������ת�����ʿɵã���ABD�ա�ACE��
��BD=CE��AB=AC��AD=AE����ABD=��ACE����BAD=��CAE��
��$\frac{AB}{AD}$=$\frac{AC}{AE}$����BAC=��DAE��
���ABC�ס�ADE��
��2���ı���CDFE�����Σ�
���ɣ���AB=AC��
���ABC=��ACB��
���ACE=��ACB��
��EF��BC��
���EFC=��ACB��
���EFC=��ACE��
��EF=EC��
��EF=CE=BD��
��BD=DC��
��EF=DC��
�֡�EF��DC��
���ı���DCEF��ƽ���ı��Σ�
��EF=EC��
��?DCEF������
��3������BAC=90��ʱ��
��AB=AC��
���ABC=��ACB=45�㣬
���ACE=��ABC=45�㣬
���DCE=90�㣬
������DCEF��������
�ʴ�Ϊ��BAC=90�㣮
���� ������Ҫ���������������ε��ж������ε��ж��������ε��ж�����ת�����ʡ����������ε��ж������ʵ�֪ʶ��֤����ACE=��EFC�����õ�EF=EC�ǽ���ڣ�2��С��Ĺؼ���

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�| A�� | -4��16��ƽ���� | B�� | $\sqrt{16}$������ƽ������4 | ||
| C�� | 0û������ƽ���� | D�� | 2��ƽ������$\sqrt{2}$ |
 ��ͼ��ij��Ԫһ�η�����ʱ����ͬһֱ������ϵ��������Ӧ������һ�κ�����ͼ����ͼ��ʾ��������Ķ�Ԫһ�η������ǣ�������
��ͼ��ij��Ԫһ�η�����ʱ����ͬһֱ������ϵ��������Ӧ������һ�κ�����ͼ����ͼ��ʾ��������Ķ�Ԫһ�η������ǣ�������| A�� | $\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{2x-y=1}\\{3x-2y=1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{2x-y=1}\\{3x+2y=5}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x+y=2}\\{3x-2y=1}\end{array}\right.$ |
| A�� |  | B�� |  | C�� |  | D�� |  |
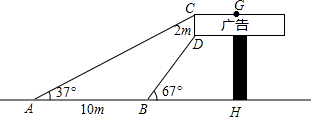 ��ѧ��ȤС����������ѧ��֪ʶ�˽�ij����Ƶĸ߶ȣ���֪CD=2m�����������õ�����������ͼ��ʾ�����С�CAH=37�㣬��DBH=67�㣬AB=10m����������������ݼ���GH�ij������ο�����sin67���$\frac{12}{13}$��cos67���$\frac{5}{13}$��tan67���$\frac{12}{5}$��cos37���$\frac{3}{5}$��sin37���$\frac{4}{5}$��tan37���$\frac{3}{4}$��
��ѧ��ȤС����������ѧ��֪ʶ�˽�ij����Ƶĸ߶ȣ���֪CD=2m�����������õ�����������ͼ��ʾ�����С�CAH=37�㣬��DBH=67�㣬AB=10m����������������ݼ���GH�ij������ο�����sin67���$\frac{12}{13}$��cos67���$\frac{5}{13}$��tan67���$\frac{12}{5}$��cos37���$\frac{3}{5}$��sin37���$\frac{4}{5}$��tan37���$\frac{3}{4}$�� ��ɽ��ij��ѧ������ȤС��������ʵ�飬���ǽ�һ�����ӵ�һ���ֲ���ˮ�У�ˮ�еĿ��ӱ����ˣ�������Ϊ�������������ɵģ���ͼ����ͼ�С�1�͡�2�ǶԶ�����Ϊʲô��
��ɽ��ij��ѧ������ȤС��������ʵ�飬���ǽ�һ�����ӵ�һ���ֲ���ˮ�У�ˮ�еĿ��ӱ����ˣ�������Ϊ�������������ɵģ���ͼ����ͼ�С�1�͡�2�ǶԶ�����Ϊʲô�� ��ͼ����һ�ų�����ֽƬABCD��EF�۵���C������C�䴦��D������D�䴦��ED�佻BC�ڵ�G����֪��EFG=50�㣮���BGD��Ķ���Ϊ80�㣮
��ͼ����һ�ų�����ֽƬABCD��EF�۵���C������C�䴦��D������D�䴦��ED�佻BC�ڵ�G����֪��EFG=50�㣮���BGD��Ķ���Ϊ80�㣮 ��ͼ����10��10�����������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���B��C����ֱ�Ϊ��-4��2������-1��2����
��ͼ����10��10�����������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���B��C����ֱ�Ϊ��-4��2������-1��2����