题目内容
5．
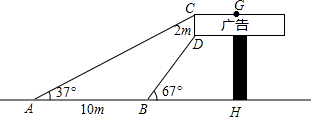数学兴趣小组想利用所学的知识了解某广告牌的高度，已知CD=2m．经测量，得到其它数据如图所示．其中∠CAH=37°，∠DBH=67°，AB=10m，请你根据以上数据计算GH的长．（参考数据sin67°≈$\frac{12}{13}$，cos67°≈$\frac{5}{13}$，tan67°≈$\frac{12}{5}$，cos37°≈$\frac{3}{5}$，sin37°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$）
分析 首先构造直角三角形，设DE=xm，则CE=（x+2）m，由三角函数得出AE和BE，由AE=BE=AB得出方程，解方程求出DE，即可得出GH的长．
解答 解：延长CD交AH于点E，如图所示：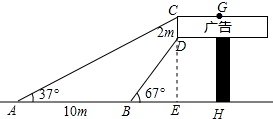
根据题意得：CE⊥AH，
设DE=xm，则CE=（x+2）m，
在Rt△AEC和Rt△BED中，tan37°=$\frac{CE}{AE}$，tan67°=$\frac{DE}{BE}$，
∴AE=$\frac{CE}{tan37°}$，BE=$\frac{DE}{tan67°}$，
∵AE-BE=AB，
∴$\frac{CE}{tan37°}$-$\frac{DE}{tan67°}$=10，
即$\frac{x+2}{\frac{3}{4}}$-$\frac{x}{\frac{12}{5}}$=10，
解得：x=8，
∴DE=8m，
∴GH=CE=CD+DE=2jm+8m=10m．
答：GH的长为10m．
点评 此题主要考查了解直角三角形的应用，根据已知构造直角三角形得出DE的长是解题关键．
练习册系列答案
相关题目
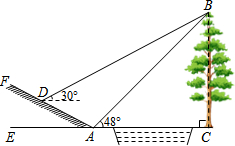如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡脚∠FAE=30°，求大树的高度．（结果保留整数，参考数据：sin48°≈0.7，cos48°≈0.7，tan48°≈1.1，$\sqrt{3}$≈1.7）
如图，在矩形ABCD中，点O是对角线AC上一点，以OC为半径的⊙O与CD交于点M，且∠BAC=∠DAM，请判断AM与⊙O的位置关系，并说明理由．
数轴上有理数a，b，c所对应的点位置如图，且b与c所对应的点到原点O的距离相等，请先判断|a+b|，|b+c|和|c-a|，再化简|a+b|+|b+c|-|c-a|．
17．已知数轴上的点A，B分别表示有理数a，b
（1）对照数轴写下表：
（2）若A，B两点间的距离记为d，试问d和a，b有何数量关系？
（3）写出所有符合条件的整数P，使它对应的点到表示10和-10的点的距离之和为20，并求所有这些整数的和．
（1）对照数轴写下表：
| a | 5 | -5 | -5 | -5 | 2 | -1.5 |
| b | 3 | 0 | 3 | -3 | -10 | 1.5 |
| A、B两点的距离 |
（3）写出所有符合条件的整数P，使它对应的点到表示10和-10的点的距离之和为20，并求所有这些整数的和．
