题目内容
5. 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(-4,2)、(-1,2).
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(-4,2)、(-1,2).(1)在图中建立平面直角坐标系,写出点A的坐标;
(2)将△ABC先向下平移4个单位,再向右平移5个单位得到△A1B1C1,画出△A1B1C1,并写出点C1的坐标;
(3)M(a,b)是△ABC内的一点,△ABC经过某种变换后点M的对应点为M2(a+1,b-7),画出△A2B2C2.并求出△A2B2C2的面积.
分析 (1)由点B、C坐标容易建立平面直角坐标系,即可得出点A的坐标;
(2)由平移的性质容易画出图形,得出点C1的坐标;
(3)把△ABC先向下平移7个单位,再向右平移1个单位,即可得出△A2B2C2,由三角形的面积公式容易求出△A2B2C2的面积.
解答 解:(1)建立平面直角坐标系,
如图1所示: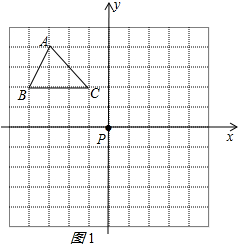
点A的坐标为( 3,4 );
(2)如图2所示: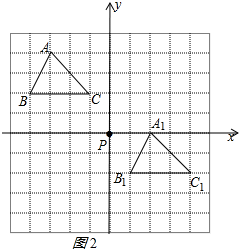
点C1的坐标为( 4,-2 );
(3)如图3所示: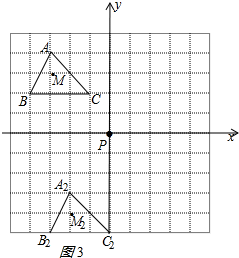
△A2B2C2的面积=$\frac{1}{2}$×3×2=3.
点评 本题考查了作图-平移变换、坐标与图形性质、三角形面积的计算;熟练掌握平移的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列运算正确的是( )
| A. | -2x2-3x2=-5x2 | B. | 6x2y3+2xy2=3xy | C. | 2x3•3x2=6x6 | D. | (a+b)2=a2-2ab+b2 |
20.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
17. 如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
 如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )| A. | $\frac{1}{3}π$-$\frac{\sqrt{3}}{4}$cm2 | B. | $\frac{\sqrt{3}}{8}$cm2 | C. | $\frac{\sqrt{3}}{2}$cm2 | D. | $\sqrt{3}$cm2 |
14.平行四边形ABCD中,∠A比∠B大40°,则∠D的度数为( )
| A. | 60° | B. | 70° | C. | 100° | D. | 110° |

 “小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.“大头儿子”稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
“小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.“大头儿子”稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.