题目内容
6.分别求出对应的二次函数的解析式:(1)已知抛物线的顶点为(-2,1),且过点(-4,3);
(2)二次函数的图象经过(-3,0)、(2,0)、(1,4)三点;
(3)已知抛物线的图象的最高点的纵坐标为6,图象经过(1,0),(-1,2).
分析 (1)根据抛物线的顶点坐标设出,抛物线的解析式为:y=a(x+2)2+1,再把(-4,3)代入,求出a的值,即可得出二次函数的解析式.
(2)已知抛物线与x轴的两个交点坐标,故设抛物线解析式为y=a(x+3)(x-2),然后把(1,4)代入,求出a的值,即可得出二次函数的解析式.
(3)设抛物线解析式为y=ax2+bx+c(a≠0),把(1,0),(-1,2)代入函数解析式,联立顶点坐标公式列出方程组,并解答.
解答 解:(1)设抛物线的解析式为:y=a(x+2)2+1(a≠0),
把(-4,3)代入解析式得a=$\frac{1}{2}$,
所以y=$\frac{1}{2}$(x+2)2+1=$\frac{1}{2}$x2+2x+3.
则抛物线的解析式为:y=$\frac{1}{2}$x2+2x+3.
(2)设抛物线解析式为y=a(x+3)(x-2)(a≠0),
把(1,4)代入解析式得:4=a(1+3)(1-2),
解得a=-1,
所以y=-(x+3)(x-2)=-x2-x+6,
则抛物线的解析式为:y=-x2-x+6.
(3)设抛物线解析式为y=ax2+bx+c(a≠0),则
$\left\{\begin{array}{l}{a+b+c=0}\\{a-b+c=2}\\{\frac{4ac-{b}^{2}}{4a}=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{-5+2\sqrt{6}}{2}}\\{b=-1}\\{c=\frac{7-2\sqrt{6}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a=\frac{-5-2\sqrt{6}}{2}}\\{b=-1}\\{c=\frac{7+2\sqrt{6}}{2}}\end{array}\right.$,
故该抛物线解析式为:y=$\frac{-5+2\sqrt{6}}{2}$x2-x+$\frac{7-2\sqrt{6}}{2}$或y=$\frac{-5-2\sqrt{6}}{2}$x2-x+$\frac{7+2\sqrt{6}}{2}$.
点评 本题主要考查了用待定系数法求二次函数解析式,解题的关键是掌握二次函数的解析式的三种形式.

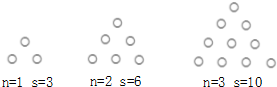 如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.