题目内容
17.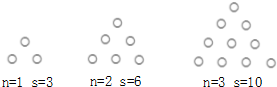 如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
分析 将n的值与s的值对应起来,找出规律,即可得出s与n的关系式.
解答 解:n=1时,s=1+2=$\frac{1}{2}$×(1+1)×(1+2)=3;
n=2时,s=1+2+3=$\frac{1}{2}$×(2+1)×(2+2)=6;
n=3时,s=1+2+3+4=$\frac{1}{2}$×(3+1)×(3+2)=10;
…
∴n=n时,s=$\frac{(n+1)(n+2)}{2}$.
故答案为:s=$\frac{(n+1)(n+2)}{2}$.
点评 此题主要考查了函数关系式以及数字规律问题,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,进而解题.

练习册系列答案
相关题目
12.如图所示图形是轴对称图形的有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.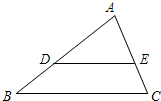 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )| A. | 4:1 | B. | 8:1 | C. | 4:9 | D. | 2:3 |
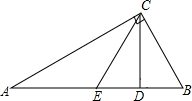 已知:如图,在△ABC中,∠A=30°,∠ACB=90°,E、D分别是AB、EB中点.求证:CD⊥AB.
已知:如图,在△ABC中,∠A=30°,∠ACB=90°,E、D分别是AB、EB中点.求证:CD⊥AB. 如图,△ABC中,AB=AC,∠B=70°.
如图,△ABC中,AB=AC,∠B=70°. 一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.
一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.