Question

9．三角形ABC中，∠A=120°，AD是角平分线，求证：$\frac{1}{AB}$+$\frac{1}{AC}$=$\frac{1}{AD}$．

Answer 1

分析 延长BA到E使AC=AE，则△ACE是等边三角形，且AD∥EC，则从而将要证的式子通分化简可证得结论．

解答 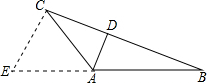解：延长BA到E使AC=AE，则△ACE是等边三角形，且AD∥EC，
∵AD∥EC，
∴△ABD∽△EBC，
∴$\frac{AD}{CE}$=$\frac{AB}{BE}$，
即$\frac{AD}{AB}$=$\frac{AC}{BE}$=$\frac{CE}{BE}$，
∴AD•BE=AB•AC，
∴$\frac{1}{AD}$=$\frac{AB+AC}{AB×AC}$=$\frac{BE}{AB×AC}$，
∴$\frac{1}{AD}$=$\frac{1}{AB}$+$\frac{1}{AC}$．

点评 本题考查了平行线的性质，难度较大，解答本题的关键是正确地作出等边三角形ACE．