题目内容
如图所示，在△ABC中D为AC边上一点，若∠DBC=∠A，BC=3，AC=6，则CD的长为（ ）| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点：相似三角形的判定与性质
专题：
分析：由∠DBC=∠A，∠C=∠C，可证得△BCD∽△ACB，所以有
=
，代入数据可求得．
| CD |
| BC |
| BC |
| AC |
解答：解：
∵∠DBC=∠A，∠C=∠C，
∴△BCD∽△ACB，
∴
=
，
∴
=
∴CD=
，
故选：C．
∵∠DBC=∠A，∠C=∠C，
∴△BCD∽△ACB，
∴
| CD |
| BC |
| BC |
| AC |
∴
| CD |
| 3 |
| 3 |
| 6 |
∴CD=
| 3 |
| 2 |
故选：C．
点评：本题主要考查相似三角形的判定和性质的应用，解题的关键是证得△BCD∽△ACB．
练习册系列答案
阅读快车系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，∠A，∠B的角平分线AD、BE交于I，AD交BC于D，BE交AC于E，若△AIB的面积为6，则四边形ABDE的面积为已知x、y是实数，并且
+y2-6y+9=0，则（xy）2013的值是（ ）
| 3x+1 |
| A、1 |
| B、-1 |
| C、0 |
| D、22013 |
已知点（3-2k2，4k-3）在第一象限的角平分线上，则k=（ ）
| A、1 | B、-1 | C、0 | D、0或1 |
使式子
有意义且取得最小值的x的取值是（ ）
| 4-x |
| A、0 | B、4 | C、2 | D、不存在 |
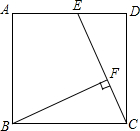如图，正方形ABCD的边长为4cm，点E为AD的中点，BF⊥EC于点F，求BF的长．