题目内容
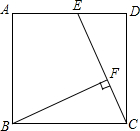 如图,正方形ABCD的边长为4cm,点E为AD的中点,BF⊥EC于点F,求BF的长.
如图,正方形ABCD的边长为4cm,点E为AD的中点,BF⊥EC于点F,求BF的长.考点:相似三角形的判定与性质,正方形的性质
专题:计算题
分析:先利用正方形的性质得BC=CD=4,DE=2,∠BCD=∠D=90°,在Rt△CDE中,根据勾股定理计算出CE=2
,再利用等角的余角相等证明∠CBF=∠DCE,则根据相似三角形的判定可判断△BCF∽△CED,然后利用相似比即可计算出BF的长.
| 5 |
解答:解:∵正方形ABCD的边长为4cm,点E为AD的中点,
∴BC=CD=4,DE=2,∠BCD=∠D=90°,
在Rt△CDE中,CE=
=2
,
∵BF⊥EC,
∴∠BFC=90°,
∴∠CBF+∠BCF=90°,
而∠DCE+∠BCF=90°,
∴∠CBF=∠DCE,
而∠BFC=∠D,
∴△BCF∽△CED,
∴BF:CD=BC:CE,即BF:4=4:2
,
∴BF=
.
∴BC=CD=4,DE=2,∠BCD=∠D=90°,
在Rt△CDE中,CE=
| DE2+CD2 |
| 5 |
∵BF⊥EC,
∴∠BFC=90°,
∴∠CBF+∠BCF=90°,
而∠DCE+∠BCF=90°,
∴∠CBF=∠DCE,
而∠BFC=∠D,
∴△BCF∽△CED,
∴BF:CD=BC:CE,即BF:4=4:2
| 5 |
∴BF=
8
| ||
| 5 |
点评:本题考查了相似三角形的判定与性质:有两组角对应相等的两个三角形相似;相似三角形对应边的比相等,都等于相似比.也考查了正方形的性质.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在平面直角坐标系中,若点P(x-2,x)在x轴上,则点P的坐标为( )
| A、(0,-2) |
| B、(0,2) |
| C、(-2,0) |
| D、(2,0) |
 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
 如图,在菱形ABCD中,AE⊥BC,E为垂足,若S菱形=60,AE=6,EC=2,P是AB边上的一个动点,则线段PE长度的最小值是
如图,在菱形ABCD中,AE⊥BC,E为垂足,若S菱形=60,AE=6,EC=2,P是AB边上的一个动点,则线段PE长度的最小值是 如图,已知每个小正方形的边长均为1,A、B、C、D是小正方形的顶点,AB、CD交于点O,求∠AOC的度数.
如图,已知每个小正方形的边长均为1,A、B、C、D是小正方形的顶点,AB、CD交于点O,求∠AOC的度数.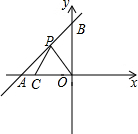 如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).
如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).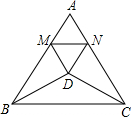 如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点做一个60°的∠MDN,点M、N分别在AB、AC上,求△AMN的周长.
如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点做一个60°的∠MDN,点M、N分别在AB、AC上,求△AMN的周长.