题目内容
已知x2+xy+9y2=1,试求x-3y的取值范围.
考点:根的判别式
专题:
分析:设x-3y=k,则x=3y+k,把x=3y+k代入x2+xy+9y2=1得:(3y+k)2+(3y+k)y+9y2=1,求出△=81k2-4×21(k2-1)≥0,即可得出答案.
解答:解:设x-3y=k,
则x=3y+k,
把x=3y+k代入x2+xy+9y2=1得:
(3y+k)2+(3y+k)y+9y2=1,
即21y2+9ky+k2-1=0有实数解,
所以△=81k2-4×21(k2-1)≥0
-3k2+84>=0
k2≤28,
-2
≤k≤2
,
即x-3y的取值范围是-2
≤k≤2
.
则x=3y+k,
把x=3y+k代入x2+xy+9y2=1得:
(3y+k)2+(3y+k)y+9y2=1,
即21y2+9ky+k2-1=0有实数解,
所以△=81k2-4×21(k2-1)≥0
-3k2+84>=0
k2≤28,
-2
| 7 |
| 7 |
即x-3y的取值范围是-2
| 7 |
| 7 |
点评:本题考查了一元二次方程根的判别式的应用,注意:一元二次方程ax2+bx+c=0,(a、b、c为常数,a≠0),当b2-4ac>0时,方程有两个不相等的实数根,当b2-4ac=0时,方程有两个相等的实数根,当b2-4ac<0时,方程无实数根.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
在下列各对整式中,是同类项的为( )
| A、3x,3y | ||
B、
| ||
| C、23,a3 | ||
| D、3m3n2,-3m2n3 |
 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
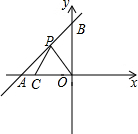 如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).
如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).