题目内容
 在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?
在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?考点:一元一次方程的应用
专题:
分析:甲每秒跑5米,则跑100米需要100÷5=20秒,连同休息的10秒共需要30秒.乙每秒跑4米,则跑100米需要100÷4=25秒,连同休息的10秒共需要35秒.35秒时,乙跑100米,甲跑100+5×5=125米,也就是有一个35秒,甲就追上乙25米.
解答:解:①甲跑100米需要时间:100÷5=20(秒);
②连同休息的10秒共需要:10+20=30(秒);
③乙跑100米需要时间:100÷4=25(秒);
④连同休息的10秒共需要:10+25=35(秒);
⑤35秒时,乙跑100米,甲跑:100+5×(35-30)=100+25=125(米);
⑥有一个35秒,甲就追上乙:125-100=25(米);
⑦A、B两点相距100米,需要几个25?
100÷25=4(个);
⑧甲追上乙需要的时间:35×4=140(秒).
答:甲追上乙需要的时间是140秒.
②连同休息的10秒共需要:10+20=30(秒);
③乙跑100米需要时间:100÷4=25(秒);
④连同休息的10秒共需要:10+25=35(秒);
⑤35秒时,乙跑100米,甲跑:100+5×(35-30)=100+25=125(米);
⑥有一个35秒,甲就追上乙:125-100=25(米);
⑦A、B两点相距100米,需要几个25?
100÷25=4(个);
⑧甲追上乙需要的时间:35×4=140(秒).
答:甲追上乙需要的时间是140秒.
点评:解决此题的关键是求出乙跑100米时,甲跑多少米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
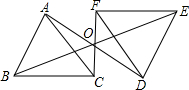 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )| A、点A与点D是对应点 |
| B、BO=EO |
| C、∠ACB=∠FDE |
| D、AB∥DE |
 已知:如图已知点P是⊙O外一点,PO交圆O于点C,OC=CP=2,点B在⊙O上,
已知:如图已知点P是⊙O外一点,PO交圆O于点C,OC=CP=2,点B在⊙O上, 如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.
如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.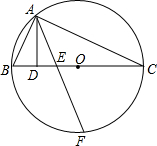 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是