题目内容
抛物线y=ax2+bx+c的对称轴是x=-2,且它与x轴的一个交点是(-3,0),则它与x轴的另一个交点是 .
考点:抛物线与x轴的交点
专题:
分析:设它与x轴的另一个交点是(x,0),再根据中点坐标公式求出x的值即可.
解答:解:设它与x轴的另一个交点是(x,0),
∵抛物线y=ax2+bx+c的对称轴是x=-2,且它与x轴的一个交点是(-3,0),
∴
=-2,解得x=-1,
∴它与x轴的另一个交点是(-1,0).
故答案为:(-1,0).
∵抛物线y=ax2+bx+c的对称轴是x=-2,且它与x轴的一个交点是(-3,0),
∴
| x-3 |
| 2 |
∴它与x轴的另一个交点是(-1,0).
故答案为:(-1,0).
点评:本题考查的是抛物线与x轴的交点,熟知抛物线与x轴的交点坐标关于抛物线的对称轴对称是解答此题的关键.

练习册系列答案
相关题目
三角形的一个顶点A,可以用数对(5,6)表示,如果把这个三角形向上平移4格,这时点A用数对( )表示.
| A、(9,6) |
| B、(5,10) |
| C、(1,6) |
| D、(5,2) |
已知⊙O的半径为10cm,如果圆心O到一条直线的距离为10cm,那么这条直线和这个圆的位置关系为( )
| A、相离 | B、相切 |
| C、相交 | D、无法确定 |
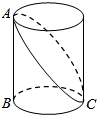 如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为
如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为 在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?
在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?