题目内容
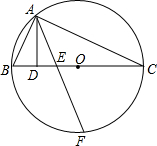 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是 |
| BC |
考点:圆周角定理,相似三角形的判定与性质
专题:
分析:连接OF、BF,则∠BOF=2∠BAF=90°,可求得BF=5
,由角平分线的性质可知
=
,且BE+CE=10,可求得BE,由条件可证得△ABF∽△BEF,可得
=
,可求得EF.
| 2 |
| AB |
| BE |
| AC |
| CE |
| AB |
| BE |
| BF |
| EF |
解答: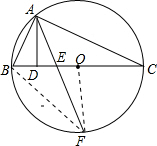 解:
解:
连接OF、BF,
∵F是
的中点,∠BAC=90°,
∴∠BAE=∠CAE=45°,
∴∠BOF=2∠BAF=90°,
在Rt△ABC中,AB=6,AC=8,可求得BC=10,
∴OB=OF=5,
∴BF=5
,
又AE平分∠BAC,
∴
=
,
∴
=
=
,且BE+CE=10,
∴BE=
,
在△ABF和△BEF中
∠EBF=∠BAF=45°,∠AFB=∠BFE,
∴△ABF∽△BEF,
∴
=
,
即
=
,
解得EF=
,
故答案为:
.
 解:
解:连接OF、BF,
∵F是
 |
| BC |
∴∠BAE=∠CAE=45°,
∴∠BOF=2∠BAF=90°,
在Rt△ABC中,AB=6,AC=8,可求得BC=10,
∴OB=OF=5,
∴BF=5
| 2 |
又AE平分∠BAC,
∴
| AB |
| BE |
| AC |
| CE |
∴
| BE |
| CE |
| 6 |
| 8 |
| 3 |
| 4 |
∴BE=
| 30 |
| 7 |
在△ABF和△BEF中
∠EBF=∠BAF=45°,∠AFB=∠BFE,
∴△ABF∽△BEF,
∴
| AB |
| BE |
| BF |
| EF |
即
| 6 | ||
|
5
| ||
| EF |
解得EF=
25
| ||
| 7 |
故答案为:
25
| ||
| 7 |
点评:本题主要考查圆周角定理及相似三角形的判定和性质,利用条件求得BE的长和证明△ABF∽△BEF是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 若有理数a、b,它们在数轴上的对应点的位置如图,把a、b、-a、-b按照从小到大的顺序排列,正确的是( )
若有理数a、b,它们在数轴上的对应点的位置如图,把a、b、-a、-b按照从小到大的顺序排列,正确的是( )| A、-b<a<-a<b |
| B、a<-b<-a<b |
| C、-b<-a<a<b |
| D、a<-a<-b<b |
 如图,在平行四边形ABCD中,O是两条对角线的交点,AC=20mm,BD=32mm,△ABO的周长等于50mm,求CD的长.
如图,在平行四边形ABCD中,O是两条对角线的交点,AC=20mm,BD=32mm,△ABO的周长等于50mm,求CD的长. 如图,在?ABCD中,对角线AC、BD交于点O,AC=
如图,在?ABCD中,对角线AC、BD交于点O,AC=
 在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?
在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒? 已知:如图,AB是⊙O的直径,直线CD交⊙O于C、D两点,过A、B两点分别作AE⊥CD、BF⊥CD,垂足为点E、F,求证:CE=DF.
已知:如图,AB是⊙O的直径,直线CD交⊙O于C、D两点,过A、B两点分别作AE⊥CD、BF⊥CD,垂足为点E、F,求证:CE=DF. 已知在△ABC中,AB=1,AC=
已知在△ABC中,AB=1,AC= 已知:如图,在⊙O中,弦AB=CD,那么∠AOC和∠BOD相等吗?请说明理由.
已知:如图,在⊙O中,弦AB=CD,那么∠AOC和∠BOD相等吗?请说明理由.