题目内容
 如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.
如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的定义可得∠ADP=∠PDF,∠CBP=∠PBA,再根据三角形的内角和定理列出等式整理即可得解.
解答:解:∵BP平分∠ABC,DP平分∠ADC,
∴∠ADP=∠PDF,∠CBP=∠PBA,
∵∠A+∠ADP=∠P+∠ABP,
∠C+∠CBP=∠P+∠PDF,
∴∠A+∠C=2∠P,
∵∠A=40°,∠C=36°,
∴∠P=
(40°+36°)=38°.
∴∠ADP=∠PDF,∠CBP=∠PBA,
∵∠A+∠ADP=∠P+∠ABP,
∠C+∠CBP=∠P+∠PDF,
∴∠A+∠C=2∠P,
∵∠A=40°,∠C=36°,
∴∠P=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.

练习册系列答案
相关题目
三角形的一个顶点A,可以用数对(5,6)表示,如果把这个三角形向上平移4格,这时点A用数对( )表示.
| A、(9,6) |
| B、(5,10) |
| C、(1,6) |
| D、(5,2) |
 如图,在?ABCD中,对角线AC、BD交于点O,AC=
如图,在?ABCD中,对角线AC、BD交于点O,AC=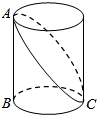 如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为
如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为 在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?
在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?