Question

20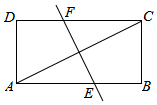．如图，将举行纸片ABCD折叠，使点A与点C重合，折痕与AB、CD分别相交于E、F，若AB=4，BC=2，那么线段AE的长为2.5．

Answer 1

分析 连接CE，根据矩形的性质得出∠B=90°，根据折叠的性质得出CE=AE，那么CE=AE=4-BE，然后在Rt△BCE中利用勾股定理求出BE=1.5，进而得出AE．

解答 解：如图，连接CE，
∵四边形ABCD是矩形，
∴∠B=90°，
由折叠得，CE=AE，
∵AB=AE+BE=4，
∴CE=AE=4-BE，
在Rt△BCE中，∵∠B=90°，BC=2，
∴CE²-BE²=BC²，
∴（4-BE）²-BE²=4，
∴BE=1.5，
∴AE=4-BE=2.5．
故答案为2.5．

点评 此题考查了图形的翻折变换，关键是掌握折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质与勾股定理．