题目内容
已知Rt△ABC三个顶点均在函数y=x2上,斜边与x轴平行,则顶点到斜边上高的取值范围为( )
| A、h=1 | B、0<h<1 |
| C、1<h≤2 | D、h>2 |
考点:二次函数的性质
专题:计算题
分析:先根据题意画出图形,再由抛物线表达式表示出A、B、C各点坐标,则可表示出线段CE、CE、DE,然后根据勾股定理得到关于h的方程,再解方程即可.
解答:解:如图,点A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴,则A、B两点关于y轴对称,
点D为斜边AB与y轴的交点,CE⊥AB与E,
 设A(-
设A(-
,b),B(
,b),C(a,a2),
则D(0,b),h=b-a2,
∵CD为斜边AB上的中线,
∴CD=
AB=
,
在Rt△CDE中,∵CE2+DE2=CD2,
∴(b-a2)2+a2=(
)2,
即(b-a2)2+a2-b=0,
即h2-h=0
解得h=1或h=0(舍去).
故选A.
点D为斜边AB与y轴的交点,CE⊥AB与E,
 设A(-
设A(-| b |
| b |
则D(0,b),h=b-a2,
∵CD为斜边AB上的中线,
∴CD=
| 1 |
| 2 |
| b |
在Rt△CDE中,∵CE2+DE2=CD2,
∴(b-a2)2+a2=(
| b |
即(b-a2)2+a2-b=0,
即h2-h=0
解得h=1或h=0(舍去).
故选A.
点评:本题考查了二次函数的性质:对于二次函数y=ax2+bx+c(a≠0),顶点坐标是(-
,
),对称轴直线x=-
.也考查了勾股定理.画出本题的大致几何图是解题的关键.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
下列命题中,真命题是( )
| A、在同一平面内,两条没有交点的射线互相平行 | ||||
| B、三角形的外角大于它的内角 | ||||
C、以
| ||||
D、∠A=
|
若m的倒数是-3,那么m的绝对值是( )
| A、3 | ||
B、-
| ||
C、
| ||
| D、-3 |
已知二次函数y=x(x-a),若当x≤2时,y随x增大而减小,当x≥2时y随x增大而增大,则a的值是( )
| A、1 | B、2 | C、4 | D、无法确定 |
 如图,把矩形ABCO放置在平面直角坐标系中,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x+6上的一点,若△APD是等腰直角三角形,则点D的坐标为
如图,把矩形ABCO放置在平面直角坐标系中,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x+6上的一点,若△APD是等腰直角三角形,则点D的坐标为 如图,在一个长方形的空地中央布置一个正方形的花坛,已知正方形的边长比长方形的长短5m,比长方形的宽短1m,且长方形的面积是正方形面积的2倍多5m2,求这个正方形的边长.
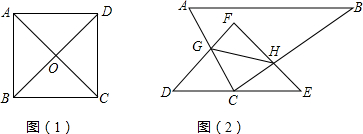
如图,在一个长方形的空地中央布置一个正方形的花坛,已知正方形的边长比长方形的长短5m,比长方形的宽短1m,且长方形的面积是正方形面积的2倍多5m2,求这个正方形的边长. 如图,A、B、D在一条直线上,△ABC与△BDE都是等边三角形,F、G、P、Q分别是AC、AD、DE、CE的中点,试判定四边形FGPQ是怎样的特殊四边形?
如图,A、B、D在一条直线上,△ABC与△BDE都是等边三角形,F、G、P、Q分别是AC、AD、DE、CE的中点,试判定四边形FGPQ是怎样的特殊四边形?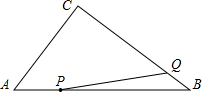 如图,在△ABC中,AB=10cm,BC=8cm,AC=6cm.动点P从点A开始在线段AB上沿A→B→A的路径以每秒2.5cm的速度运动,同时动点Q从点B开始在线段BC上以每秒1cm的速度向点C运动,设点P,Q运动的时间为t秒(0<t<8).
如图,在△ABC中,AB=10cm,BC=8cm,AC=6cm.动点P从点A开始在线段AB上沿A→B→A的路径以每秒2.5cm的速度运动,同时动点Q从点B开始在线段BC上以每秒1cm的速度向点C运动,设点P,Q运动的时间为t秒(0<t<8).