题目内容
 如图,在△ABC中,D为BC上一点,BD=CD,AD⊥AC于点A,∠BAD=30°.
如图,在△ABC中,D为BC上一点,BD=CD,AD⊥AC于点A,∠BAD=30°.(1)求证:AC=
| 1 |
| 2 |
(2)当AB=4,AD=
| 3 |
考点:直角三角形斜边上的中线
专题:
分析:(1)延长AD到E,使DE=AD,然后利用“边角边”证明△ACD和△EBD全等,根据全等三角形对应边相等可得BE=AC,全等三角形对应角相等可得∠E=∠CAD,再根据直角三角形30°角所对的直角边等于斜边的一半证明;
(2)求出BE,然后利用三角形的面积公式列式计算即可得解.
(2)求出BE,然后利用三角形的面积公式列式计算即可得解.
解答: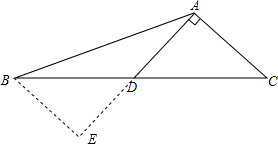 (1)证明:如图,延长AD到E,使DE=AD,
(1)证明:如图,延长AD到E,使DE=AD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴BE=AC,∠E=∠CAD=90°,
∵∠BAD=30°,
∴BE=
AB,
∴AC=
AB;
(2)解:∵AB=4,
∴BE=
×4=2,
∴S△ABD=
AD•BE=
×
×=
.
 (1)证明:如图,延长AD到E,使DE=AD,
(1)证明:如图,延长AD到E,使DE=AD,在△ACD和△EBD中,
|
∴△ACD≌△EBD(SAS),
∴BE=AC,∠E=∠CAD=90°,
∵∠BAD=30°,
∴BE=
| 1 |
| 2 |
∴AC=
| 1 |
| 2 |
(2)解:∵AB=4,
∴BE=
| 1 |
| 2 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,全等三角形的判定与性质,“遇中线,加倍延”作辅助线,构造出全等三角形是解题的关键.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、在同一平面内,两条没有交点的射线互相平行 | ||||
| B、三角形的外角大于它的内角 | ||||
C、以
| ||||
D、∠A=
|
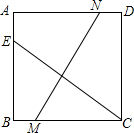 已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数.
已知:如图,正方形ABCD中,点E、M、N分别在AB、BC、AD边上,CE=MN,∠MCE=35°,求∠ANM的度数. 东山宾馆主楼梯准备铺上红地毯,已知这种地毯每平方米造价为25元,主楼梯宽2m,侧面如图所示,则购买这种地毯至少需要
东山宾馆主楼梯准备铺上红地毯,已知这种地毯每平方米造价为25元,主楼梯宽2m,侧面如图所示,则购买这种地毯至少需要 某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由.
某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由. 如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?
如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD? 如图是某几何体的展开图
如图是某几何体的展开图