题目内容
 如图,大圆O1的半径O1A是小圆O2的直径,⊙O1的另一半O1C交⊙O2于B.求证:
如图,大圆O1的半径O1A是小圆O2的直径,⊙O1的另一半O1C交⊙O2于B.求证: |
| AB |
 |
| AC |
考点:弧长的计算
专题:证明题
分析:根据圆周角定理和弧长公式进行计算,从而证得结论.
解答: 证明:如图,连接BO2.则∠BO2A=2∠BO1A.
证明:如图,连接BO2.则∠BO2A=2∠BO1A.
设AO1=2r,∠BO1A=α,则∠BO2A=2α.
所以
的长度=
=
,
的长度=
=
,
故
与
的长相等.
 证明:如图,连接BO2.则∠BO2A=2∠BO1A.
证明:如图,连接BO2.则∠BO2A=2∠BO1A.设AO1=2r,∠BO1A=α,则∠BO2A=2α.
所以
 |
| AB |
| 2α•π•r |
| 180 |
| παr |
| 180 |
 |
| AC |
| α•π×2r |
| 180 |
| παr |
| 180 |
故
 |
| AB |
 |
| AC |
点评:本题主要考查了圆周角定理以及弧长的计算公式,根据大圆的弧长得出小圆的圆心角是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,真命题是( )
| A、在同一平面内,两条没有交点的射线互相平行 | ||||
| B、三角形的外角大于它的内角 | ||||
C、以
| ||||
D、∠A=
|
 某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由.
某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由. 如图,△DEF是△ABC平移后的图形,点D是点A的对应点.
如图,△DEF是△ABC平移后的图形,点D是点A的对应点.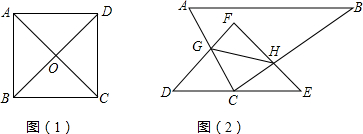
 如图,把矩形ABCO放置在平面直角坐标系中,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x+6上的一点,若△APD是等腰直角三角形,则点D的坐标为
如图,把矩形ABCO放置在平面直角坐标系中,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x+6上的一点,若△APD是等腰直角三角形,则点D的坐标为 如图,A、B、D在一条直线上,△ABC与△BDE都是等边三角形,F、G、P、Q分别是AC、AD、DE、CE的中点,试判定四边形FGPQ是怎样的特殊四边形?
如图,A、B、D在一条直线上,△ABC与△BDE都是等边三角形,F、G、P、Q分别是AC、AD、DE、CE的中点,试判定四边形FGPQ是怎样的特殊四边形?