题目内容
12.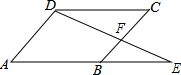 如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.
如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.
分析 由AE=4BE结合平行四边形的性质可得$\frac{BE}{AB}=\frac{BE}{CD}=\frac{1}{3}$,根据CD∥AE知△CDF∽△BEF,由相似三角形性质可得答案.
解答 解:∵AE=4BE,
∴$\frac{BE}{AB}=\frac{1}{3}$,
∵四边形ABCD是平行四边形,
∴AB=CD,CD∥AE,
∴△CDF∽△BEF,$\frac{BE}{AB}=\frac{BE}{CD}=\frac{1}{3}$,
∴$\frac{BF}{FC}=\frac{BE}{CD}=\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题主要考查相似三角形的判定与性质及平行四边形的性质,由AE=4BE根据平行四边形性质得$\frac{BE}{CD}$的值是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
2.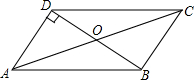 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
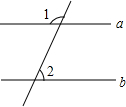 如图,a∥b,∠1=130°,则∠2=50°.
如图,a∥b,∠1=130°,则∠2=50°. 如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).
如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).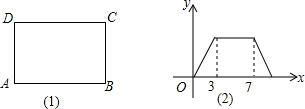
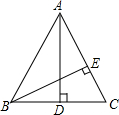 如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.
如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.