题目内容
7.解不等式组$\left\{\begin{array}{l}{2x-3<x}\\{x+2≥-\frac{1}{2}x-1}\end{array}\right.$,并写出不等式的正整数解.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式2x-3<x,得:x<3,
解不等式x+2≥-$\frac{1}{2}$x-1,得:x≥-2,
∴-2≤x<3,
∵x为正整数,
∴x=1或x=2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
15.下列等式从左到右的变形属于因式分解的是( )
| A. | x2-x-6=(x-3)(x+2) | B. | (x+4)(x-3)=x2+x-12 | ||
| C. | x2-9+6x=(x+3)(x-3)+6x | D. | 10ab=2a•5b |
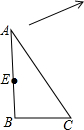 把下图所示的三角形ABC
把下图所示的三角形ABC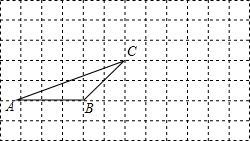 如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).
如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).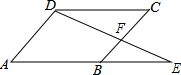 如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.
如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.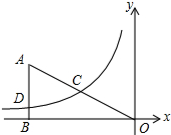 如图,在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,联结AO得到△AOB,过边AO中点C的反比例函数$y=\frac{k}{x}$的图象与边AB交于点D.求:
如图,在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,联结AO得到△AOB,过边AO中点C的反比例函数$y=\frac{k}{x}$的图象与边AB交于点D.求: 阅读下面材料:
阅读下面材料: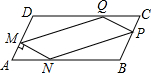 在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.
在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.