题目内容
等腰三角形的两个外角的度数比为2:5,则它的顶角的度数是( )
| A、40° | B、120° |
| C、140° | D、40°或140° |
考点:等腰三角形的性质
专题:
分析:先设这两个外角等于2x,5x,然后分类讨论,①若底角的外角是2x;②若顶角的外角是2x,再结合三角形内角和定理可求x,从而求出其它角的度数.
解答:解:设这两个外角等于2x,5x,
①若底角的外角是2x,则有2(180°-2x)+(180°-5x)=180°,
解得x=40°,
则底角=100°,不合题意,舍去.
②若顶角的外角是2x,则有(180°-2x)+2(180°-5x)=180°,
解得x=30°,
则顶角=120°,那么底角=30°,
故选:B.
①若底角的外角是2x,则有2(180°-2x)+(180°-5x)=180°,
解得x=40°,
则底角=100°,不合题意,舍去.
②若顶角的外角是2x,则有(180°-2x)+2(180°-5x)=180°,
解得x=30°,
则顶角=120°,那么底角=30°,
故选:B.
点评:本题考查等腰三角形的性质,三角形内角和定理及三角形外角性质等知识;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.

练习册系列答案
相关题目
 如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).
如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).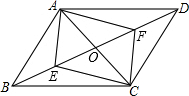 如图,在平行四边形ABCD中AC,BD相交于点O,E,F分别是OB、OD的中点.
如图,在平行四边形ABCD中AC,BD相交于点O,E,F分别是OB、OD的中点. 如图所示,已知点O是∠ABC,∠ACB的平分线的交点,且OD∥AB,OE∥AC.
如图所示,已知点O是∠ABC,∠ACB的平分线的交点,且OD∥AB,OE∥AC.
 在△ABC中,边BC的长与BC边上的高线长之和为20.
在△ABC中,边BC的长与BC边上的高线长之和为20. 观察下面图形,并回答问题.
观察下面图形,并回答问题.