题目内容
 如图所示,已知点O是∠ABC,∠ACB的平分线的交点,且OD∥AB,OE∥AC.
如图所示,已知点O是∠ABC,∠ACB的平分线的交点,且OD∥AB,OE∥AC.(1)图中共有几个等腰三角形?并选一个进行证明.
(2)试说明△ODE的周长与BC的关系.
(3)若BC=12cm,求△ODE的周长.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)由OB,OC分别是△ABC的∠ABC和∠ACB的平分线和OE∥AB、OF∥AC可推出BE=OE,OF=FC;
(2)由(1)的结论可知,△ODE的周长即为BC的长度;
(3)把相关数据代入(2)中的等式进行计算即可.
(2)由(1)的结论可知,△ODE的周长即为BC的长度;
(3)把相关数据代入(2)中的等式进行计算即可.
解答:解:(1)图中共有2个等腰三角形:△OBD、△OEC.理由如下:
∵OD∥AB,
∴∠ABO=∠BOD.
∵OB平分∠ABC,
∴∠ABO=∠OBD,
∴∠ABO=∠BOD,
∴BD=OD,
则同理可得CE=OE,
∴△OBD和△OEC是等腰三角形.
(2)△ODE的周长即为BC的长度.理由如下:
由(1)知,BD=OD,CE=OE,则
△ODE的周长=OD+DE+OE=BD+DE+EC=BC,即△ODE的周长即为BC的长度.
(3)由(2)知,△ODE的周长=BC,
∵BC=12cm,
∴△ODE的周长=12cm.
∵OD∥AB,
∴∠ABO=∠BOD.
∵OB平分∠ABC,
∴∠ABO=∠OBD,
∴∠ABO=∠BOD,
∴BD=OD,
则同理可得CE=OE,
∴△OBD和△OEC是等腰三角形.
(2)△ODE的周长即为BC的长度.理由如下:
由(1)知,BD=OD,CE=OE,则
△ODE的周长=OD+DE+OE=BD+DE+EC=BC,即△ODE的周长即为BC的长度.
(3)由(2)知,△ODE的周长=BC,
∵BC=12cm,
∴△ODE的周长=12cm.
点评:本题考查了平行线的性质,以及等腰三角形的判定方法,正确证得OD=BD,CE=OE是关键.

练习册系列答案
相关题目
10名学生的体重(单位:㎏)分别是41,48,50,53,49,50,53,53,51,67,这组数据的众数是( )
| A、50 | B、51 | C、52 | D、53 |
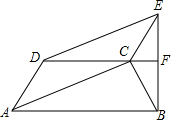 如图,四边形ACED为平行四边形,DF垂直平分BE甲乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )
如图,四边形ACED为平行四边形,DF垂直平分BE甲乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )| A、甲虫先到 | B、乙虫先到 |
| C、两虫同时到 | D、无法确定 |
等腰三角形的两个外角的度数比为2:5,则它的顶角的度数是( )
| A、40° | B、120° |
| C、140° | D、40°或140° |
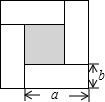 如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )| A、a2-b2=(a+b)(a-b) |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=(a+b)2-4ab |
| D、a2+ab=a(a+b) |

 如图,已知∠AOC=∠BOD=110°,∠BOC=75°,求:∠AOD的度数.
如图,已知∠AOC=∠BOD=110°,∠BOC=75°,求:∠AOD的度数.