题目内容
 在△ABC中,边BC的长与BC边上的高线长之和为20.
在△ABC中,边BC的长与BC边上的高线长之和为20.(1)写出△ABC的面积y与BC的长x之间的函数关系式.并写出自变量X的取值范围.
(2)当BC的长为多少时,△ABC的面积最大?最大面积是多少?
考点:二次函数的应用
专题:
分析:(1)直接利用三角形面积求法得出即可;
(2)利用配方法求出二次函数最值进而得出答案.
(2)利用配方法求出二次函数最值进而得出答案.
解答:解;(1)由题意可得:
y=
x(20-x)=-
x2+10x(0<x<20);
(2)由(1)得,
y=-
x2+10x
=-
(x-10)2+50
∵a=-
<0,x=10在0<x<20的范围内,
∴当x=10时,y最大=50,
即当BC的长为10时,△ABC的面积最大为50.
y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)得,
y=-
| 1 |
| 2 |
=-
| 1 |
| 2 |
∵a=-
| 1 |
| 2 |
∴当x=10时,y最大=50,
即当BC的长为10时,△ABC的面积最大为50.
点评:此题主要考查了二次函数的应用,正确运用配方法求出二次函数最值是解题关键.

练习册系列答案
相关题目
有关近似数3.210×104的叙述正确的是( )
| A、精确到千分位 |
| B、精确到百分位 |
| C、精确到百位 |
| D、精确到十位 |
等腰三角形的两个外角的度数比为2:5,则它的顶角的度数是( )
| A、40° | B、120° |
| C、140° | D、40°或140° |
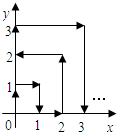 如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )
如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )| A、(0,9) |
| B、(9,0) |
| C、(0,8) |
| D、( 8,0) |
在同一平面直角坐标系中,同一水平线上开口最大的抛物线是( )
| A、y=-x2 | ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
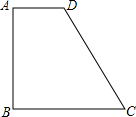 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=3,BC=4,则CD的长是
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=3,BC=4,则CD的长是