题目内容
17．已知关于x的不等式组$\left\{\begin{array}{l}{5x+2＞3（x-1）}\\{\frac{1}{2}x≤8-\frac{3}{2}x+2a}\end{array}\right.$有四个整数解，则实数a的取值范围是-3≤a＜-2．分析 别求出不等式组中两不等式的解集，根据不等式组有四个整数解，即可确定出a的范围．
解答 解：$\left\{\begin{array}{l}{5x+2＞3（x-1）①}\\{\frac{1}{2}x≤8-\frac{3}{2}x+2a②}\end{array}\right.$
解不等式①得：x＞-$\frac{5}{2}$，
解不等式②得：x≤a+4，
∴-$\frac{5}{2}$＜x≤a+4
∵不等式组有四个整数解，
∴不等式组的整数解为：-2，-1，0，1
∴1≤a+4＜2，
解得：-3≤a＜-2．
故答案为：-3≤a＜-2．
点评 此题考查了一元一次不等式组的整数解，熟练掌握运算法则是解本题的关键．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
7．
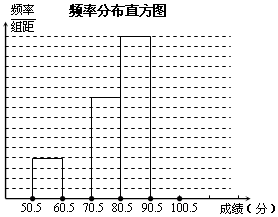为了让学生了解环保知识，增强环保意识．某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成的频数分布表和频数分布直方图，解答下列问题：
频数分布表
（1）频数分布表中a=12；b=50；
（2）补全频数分布直方图；（3）在该问题中的样本容量是50；
（4）全体参赛学生中，竞赛成绩落在80.5～90.5组范围内的人数最多；
（5）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为216人．
为了让学生了解环保知识，增强环保意识．某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成的频数分布表和频数分布直方图，解答下列问题：频数分布表
| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 008 |
| 60.5～70.5 | 8 | b |
| 70.5～80.5 | 10 | 020 |
| 80.5～90.5 | 16 | 032 |
| 90.5～100.5 | a | 0.24 |
| 合计 |
（2）补全频数分布直方图；（3）在该问题中的样本容量是50；
（4）全体参赛学生中，竞赛成绩落在80.5～90.5组范围内的人数最多；
（5）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为216人．
如图，直线a∥b，∠1=70°，∠2=35°，则∠3的度数是35°．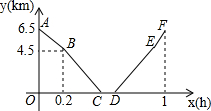
从甲地到乙地，先是一段上坡路，然后是一段平路，小明骑车从甲地出发，到达乙地后休息一段时间，然后原路返回甲地，假设小明骑车在上坡、平路、下坡时分别保持匀速前进，已知小明骑车上坡的速度比平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km，小明出发时间为x（单位：h），距乙地的距离为y（单位：km），图中的折线ABCDEF表示y与x之间的函数关系．
如图，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．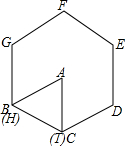
正△ABC与正六边形DEFGH的边长相等，初始如图所示，将三角形绕点I顺时针旋转使得AC与CD重合，再将三角形绕点D顺时针旋转使得AB与DE重合，…，按这样的方式将△ABC旋转2015次后，△ABC中与正六边形DEFGHI重合的边是（ ）