题目内容
12.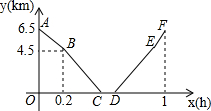 从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地,假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,小明出发时间为x(单位:h),距乙地的距离为y(单位:km),图中的折线ABCDEF表示y与x之间的函数关系.
从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地,假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,小明出发时间为x(单位:h),距乙地的距离为y(单位:km),图中的折线ABCDEF表示y与x之间的函数关系.(1)小明骑车在平路上的速度为15km/h;
(2)小明在乙地休息了0.1h;
(3)分别求线段AB、EF所对应的函数解析式;
(4)求小明开始走下坡路的时间;
(5)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的距离.
分析 (1)先计算出小明骑车上坡的速度,再根据骑车上坡的速度比平路上的速度每小时少5km求出小明平路上的速度;
(2)求出小明下坡的速度,平路上所用的时间,下坡所用的时间,那么小明在乙地休息的时间=1h-小明上坡所用的时间0.2h-平路上所用的时间-下坡所用的时间;
(3)根据上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:yAB=6.5-10x,线段EF所对应的函数关系式为yEF=4.5+20(x-0.9),即可解答;
(4)根据图象可知点E处对应的时间开始走下坡路,进而求解;
(5)设小明出发a小时第一次经过丙地,根据题意得到6.5-10a=20(a+0.85)-13.5,求出a的值,即可解答.
解答 解:(1)小明骑车上坡的速度为:(6.5-4.5)÷0.2=10(km/h),
平路上的速度为:10+5=15(km/h),
故答案为:15;
(2)下坡的速度为:15+5=20(km/h),
平路上所用的时间为:2(4.5÷15)=0.6h,
下坡所用的时间为:(6.5-4.5)÷20=0.1h
所以小明在乙地休息了:1-0.1-0.6-0.2=0.1(h).
故答案为:0.1;
(3)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,
所以线段AB所对应的函数关系式为:y=6.5-10x,
即yAB=-10x+6.5(0≤x≤0.2).
线段EF所对应的函数关系式为yEF=4.5+20(x-0.9).
即yEF=20x-13.5(0.9≤x≤1);
(4)由题意知小明在点E处对应的时间开始走下坡路,
所以开始走下坡路的时间为0.2+0.1+0.6=0.9(h);
(5)由题意可知:小明第一次经过丙地在AB段,第二次经过丙地在EF段,
设小明出发a小时第一次经过丙地,则小明出发后(a+0.85)小时第二次经过丙地,
6.5-10a=20(a+0.85)-13.5,
解得:a=$\frac{1}{10}$.
$\frac{1}{10}$×10=1(千米).
答:丙地与甲地之间的距离为1千米.
点评 本题考查了一次函数的应用,行程问题数量关系的运用,一次函数解析式的确定,一元一次方程的运用.解决本题的关键是读懂函数图象,求出一次函数的解析式.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 如图,E、F分别是正方形ABCD的边CD、AD上的点,CE=DF,AE、BF相交于点O.下列结论:(1)AE=BF;(2)AE⊥BF;(3)△ABF与△DAE成中心对称.其中,正确的结论有( )
如图,E、F分别是正方形ABCD的边CD、AD上的点,CE=DF,AE、BF相交于点O.下列结论:(1)AE=BF;(2)AE⊥BF;(3)△ABF与△DAE成中心对称.其中,正确的结论有( ) 如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).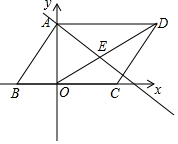 如图,平行四边形ABCD在直角坐标系中,tan∠ABC=$\frac{4}{3}$,AD=6,OA的长是方程x2-x-12=0的一个根,E是线段OD的中点.
如图,平行四边形ABCD在直角坐标系中,tan∠ABC=$\frac{4}{3}$,AD=6,OA的长是方程x2-x-12=0的一个根,E是线段OD的中点. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).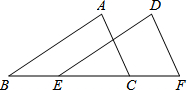 如图,点B、E、C、F在同一条直线上,且BE=CF,AB∥DE,AC∥DF,求证:AB=DE.
如图,点B、E、C、F在同一条直线上,且BE=CF,AB∥DE,AC∥DF,求证:AB=DE.