题目内容
6.先化简,再求值:$\frac{3}{x-2}$-$\frac{x-3}{{{x^2}-4}}$÷$\frac{{{x^2}-x-6}}{{{x^2}+4x+4}}$,其中x=$\sqrt{3}$+3.分析 根据分式的减法和除法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:$\frac{3}{x-2}$-$\frac{x-3}{{{x^2}-4}}$÷$\frac{{{x^2}-x-6}}{{{x^2}+4x+4}}$
=$\frac{3}{x-2}-\frac{x-3}{(x+2)(x-2)}•\frac{(x+2)^{2}}{(x-3)(x+2)}$
=$\frac{3}{x-2}-\frac{1}{x-2}$
=$\frac{2}{x-2}$,
当x=$\sqrt{3}$+3时,原式=$\frac{2}{\sqrt{3}+3-2}=\sqrt{3}-1$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
11.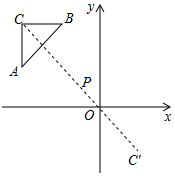 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,0) | B. | (2,-1) | C. | (0,-2) | D. | (1,-2) |
16.五边形的对角线共有( )条.
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).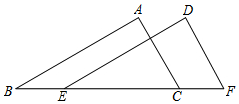 如图,在△ABC和△DEF中,B、E、C、F在同一直线上,已知AB=DE,AC=DF,BE=CF.求证:AB∥DE.
如图,在△ABC和△DEF中,B、E、C、F在同一直线上,已知AB=DE,AC=DF,BE=CF.求证:AB∥DE. 正八边形ABCDEFGH的半径为$\sqrt{2}$cm,则它的面积为8$\sqrt{2}$cm2.
正八边形ABCDEFGH的半径为$\sqrt{2}$cm,则它的面积为8$\sqrt{2}$cm2.