题目内容
 反比例函数y=
反比例函数y=| 2m-1 |
| x |
(1)求m的取值范围;
(2)点(-1,-3)和(3,n)在这个反比例函数图象上,求m和n的值.
考点:反比例函数图象上点的坐标特征,反比例函数的性质
专题:计算题
分析:(1)根据反比例函数的性质得2m-1>0,然后解不等式即可;
(2)根据反比例函数图象上点的坐标特征得到2m-1=-1×(-3)=3n,然后解方程即可得到m和n的值.
(2)根据反比例函数图象上点的坐标特征得到2m-1=-1×(-3)=3n,然后解方程即可得到m和n的值.
解答:解:(1)∵反比例函数图象分布在第一、三象限,
∴2m-1>0,
∴m>
;
(2)∵点(-1,-3)和(3,n)在这个反比例函数图象上,
∴2m-1=-1×(-3)=3n,
∴m=2,n=1.
∴2m-1>0,
∴m>
| 1 |
| 2 |
(2)∵点(-1,-3)和(3,n)在这个反比例函数图象上,
∴2m-1=-1×(-3)=3n,
∴m=2,n=1.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.
| k |
| x |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面的说法中,正确的个数有( )
①柱体的两个底面一样大 ②圆柱、圆锥的底面都是圆 ③棱柱的底面是四边形
④棱柱的侧面一定是长方形(包括正方形) ⑤长方体一定是柱体 ⑥长方体的面不可能是正方形.
①柱体的两个底面一样大 ②圆柱、圆锥的底面都是圆 ③棱柱的底面是四边形
④棱柱的侧面一定是长方形(包括正方形) ⑤长方体一定是柱体 ⑥长方体的面不可能是正方形.
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,方格纸上的每个小方格都是边长为1 的正方形,△ABC的顶点均在格点上,若B点的坐标为(-4,-2)按要求回答下列问题
如图,方格纸上的每个小方格都是边长为1 的正方形,△ABC的顶点均在格点上,若B点的坐标为(-4,-2)按要求回答下列问题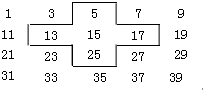 将连续的奇数1,3,5,7,9…排成如下的数表:
将连续的奇数1,3,5,7,9…排成如下的数表: