题目内容
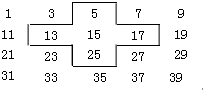 将连续的奇数1,3,5,7,9…排成如下的数表:
将连续的奇数1,3,5,7,9…排成如下的数表:(1)十字框中的五个数的平均数与15有什么关系?
(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.
考点:一元一次方程的应用
专题:
分析:(1)先算出十字框中的五个数的平均数,然后判断与15的关系;
(2)设中间的数是x,表示出其余4个数,然后列出方程并求解,再根据x是奇数且前后都有奇数解答.
(2)设中间的数是x,表示出其余4个数,然后列出方程并求解,再根据x是奇数且前后都有奇数解答.
解答:解:(1)相等.
(5+13+15+17+25)÷5=15,
故十字框中的五个数的平均数等于15;
(2)能.
设中间的数是x,则其余4个数分别为x-10,x-2,x+2,x+10,
则这五个数的和=x-10+x-2+x+x+2+x+10=5x,
5x=315,
解得,x=63,
由图可知,63排在最左边的第二列,所以,不可能成为十字框最中间的一个数.
(5+13+15+17+25)÷5=15,
故十字框中的五个数的平均数等于15;
(2)能.
设中间的数是x,则其余4个数分别为x-10,x-2,x+2,x+10,
则这五个数的和=x-10+x-2+x+x+2+x+10=5x,
5x=315,
解得,x=63,
由图可知,63排在最左边的第二列,所以,不可能成为十字框最中间的一个数.
点评:本题考查了一元一次方程的应用.仔细阅读图表排列规律,观察出其余四个数与最中间的数的关系是解题的关键.

练习册系列答案
相关题目
如果不等式组
无解,则a的取值范围是( )
|
| A、a<1 | B、a≤1 |
| C、a>1 | D、a≥1 |
下列各式中,一定属于二次根式的是( )
A、
| |||
B、
| |||
C、
| |||
D、
|
 已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,BM是线段CF的垂直平分线,垂足为M.N是线段BM上一点,且NC=EF.
已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,BM是线段CF的垂直平分线,垂足为M.N是线段BM上一点,且NC=EF. 反比例函数y=
反比例函数y=