题目内容
20.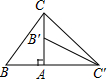 如图,在直角三角形ABC中,∠BAC=90°,∠B=60°,AC=3,将三角形ABC绕点A按顺时针方向旋转90°,得到直角三角形AB'C'(点B'与点B是对应点,点C'与点C是对应点),连接CC',则AC'=3,∠AC'B'=30°,∠AC'C=45°.
如图,在直角三角形ABC中,∠BAC=90°,∠B=60°,AC=3,将三角形ABC绕点A按顺时针方向旋转90°,得到直角三角形AB'C'(点B'与点B是对应点,点C'与点C是对应点),连接CC',则AC'=3,∠AC'B'=30°,∠AC'C=45°.
分析 根据直角三角形ABC中,∠BAC=90°,∠B=60°,即可得出∠ACB=30°,再根据旋转的性质,即可得到AC'=AC=3,∠AC'B'=∠ACB=30°,∠CAC'=90°,即可得到△CAC'是等腰直角三角形,据此可得∠AC'C=45°.
解答 解:∵直角三角形ABC中,∠BAC=90°,∠B=60°,
∴∠ACB=30°,
∵将三角形ABC绕点A按顺时针方向旋转90°,得到直角三角形AB'C',
∴AC'=AC=3,∠AC'B'=∠ACB=30°,∠CAC'=90°,
∴△CAC'是等腰直角三角形,
∴∠AC'C=45°,
故答案为:3,30°,45°.
点评 本题主要考查了旋转的性质,等腰直角三角形的判定与性质的运用,解题时注意:旋转前、后的图形全等;对应点与旋转中心所连线段的夹角等于旋转角.

练习册系列答案
相关题目
5.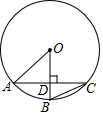 如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
 如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}-1$ |
12.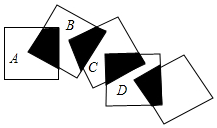 将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )
将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )
 将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )
将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
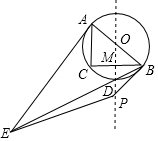 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,圆O是△ABC的外接圆,点M是CB的中点,连接OM并延长交劣弧$\widehat{BC}$于点D,连接BD并延长与过点A的切线交于点E,P是直线OD上一个动点,当|PE-PB|有最大值时,PD的长度是$\frac{165}{74}$.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,圆O是△ABC的外接圆,点M是CB的中点,连接OM并延长交劣弧$\widehat{BC}$于点D,连接BD并延长与过点A的切线交于点E,P是直线OD上一个动点,当|PE-PB|有最大值时,PD的长度是$\frac{165}{74}$.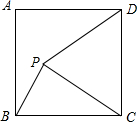 如图,正方形ABCD的边长为4,点P为正方形内部(含边上)的任意一点,且BP=2,分别连接PC、PD,则PD+$\frac{1}{2}$PC的最小值为5.
如图,正方形ABCD的边长为4,点P为正方形内部(含边上)的任意一点,且BP=2,分别连接PC、PD,则PD+$\frac{1}{2}$PC的最小值为5.