题目内容
1. 如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.
如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.
分析 延长AD,由平行线的性质得出∠EDC=∠DCB,证明A、B、C、D四点共圆,由圆周角定理得出∠EDC=∠ABC,∠BAC=∠CDB,证出∠ABC=∠DCB,由AAS证明△ABC≌△DCB,得出对应边相等即可.
解答 证明:延长AD,如图所示: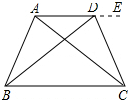
∵AD∥BC,
∴∠EDC=∠DCB,
∵∠ABD=∠ACD,
∴A、B、C、D四点共圆,
∴∠EDC=∠ABC,∠BAC=∠CDB,
∴∠ABC=∠DCB,
在△ABC和△DCB中,$\left\{\begin{array}{l}{∠BAC=∠CDB}&{\;}\\{∠ABC=∠DCB}&{\;}\\{BC=CB}&{\;}\end{array}\right.$,
∴△ABC≌△DCB(AAS),
∴AB=DC.
点评 本题考查了全等三角形的判定与性质、梯形的性质、四点共圆、圆周角定理等知识;本题有一定难度,需要通过证明四点共圆得出角相等才能证明三角形全等.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11.三角形各边长度如下,其中不是直角三角形的是( )
| A. | 20、21、29 | B. | 16、28、34 | C. | 3、4、5 | D. | 5、12、13 |
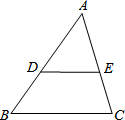 如图,在△ABC中,DE∥BC,AD=3cm,BD=2cm,则△ADE与△ABC的相似比为$\frac{3}{5}$.
如图,在△ABC中,DE∥BC,AD=3cm,BD=2cm,则△ADE与△ABC的相似比为$\frac{3}{5}$.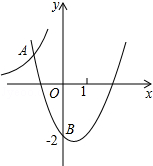 如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-$\frac{12}{x}$的图象交于点A(m,4),求这个二次函数的解析式.
如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-$\frac{12}{x}$的图象交于点A(m,4),求这个二次函数的解析式.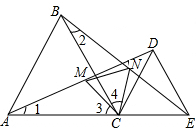 如图,已知点A、C、E在同一直线上,△ABC和△CDE都是等边三角形,M、N分别为AD、BE的中点,求证:△CMN是等边三角形.
如图,已知点A、C、E在同一直线上,△ABC和△CDE都是等边三角形,M、N分别为AD、BE的中点,求证:△CMN是等边三角形.
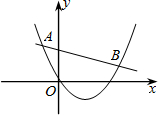 如图所示,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).根据图象回答:
如图所示,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).根据图象回答: