题目内容
10.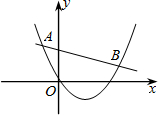 如图所示,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).根据图象回答:
如图所示,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).根据图象回答:(1)方程ax2+bx+c=kx+m的解是x1=-2,x2=8;
(2)方程组$\left\{\begin{array}{l}{y=a{x}^{2}+bx+c}\\{y=kx+m}\end{array}\right.$的解是$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=8}\\{{y}_{2}=2}\end{array}\right.$;
(3)当x满足x<-2或x>8时,y1>y2;
(4)当x满足-2<x<8时,y2<y1.
分析 (1)方程的解就是两个函数交点的横坐标,据此即可求解;
(2)两个函数交点的坐标就是方程组的解;
(3)当y1的图象在y2的图象的上边时对应的自变量的取值范围;
(4)求当y1的图象在y2的图象的下边时对应的自变量的取值范围
解答 解:(1)程ax2+bx+c=kx+m的解是x1=-2,x2=8;
故答案是:x1=-2,x2=8;
(2)方程组$\left\{\begin{array}{l}{y=a{x}^{2}+bx+c}\\{y=kx+m}\end{array}\right.$的解是$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=8}\\{{y}_{2}=2}\end{array}\right.$.
故答案是:是$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=8}\\{{y}_{2}=2}\end{array}\right.$.
(3)当x<-2或x>8时,y1>y2.
故答案是:x<-2或x>8;
(4)当-2<x<8时,y2<y1.
故答案是:-2<x<8.
点评 本题考查了二次函数与不等式的关系,理解函数解析式就是方程,函数图象上点的坐标就是方程的解是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.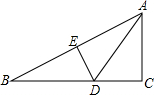 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )| A. | 3cm | B. | 4.5cm | C. | 6cm | D. | 7.5cm |
15.请观察:13+23=9=(1+2)2,13+23+33=36=(1+2+3)2,那么13+23+33+43+53等于( )
| A. | 15 | B. | 115 | C. | 225 | D. | 625 |
 如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.
如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.
 已知,如图,四边形ABCD中.AB=AD,CB=CD,AC与BD交于点E.求证:
已知,如图,四边形ABCD中.AB=AD,CB=CD,AC与BD交于点E.求证:
 如图,D是AC上一点,DE∥AB,∠B=∠DAE.求证:△ABC∽△DAE.
如图,D是AC上一点,DE∥AB,∠B=∠DAE.求证:△ABC∽△DAE.