题目内容
1.在△ABC中,∠B=30°,AB=12,AC=6,则BC=6$\sqrt{3}$.分析 由∠B=30°,AB=12,AC=6,利用30°所对的直角边等于斜边的一半易得△ABC是直角三角形,利用勾股定理求出BC的长.
解答 解:∵∠B=30°,AB=12,AC=6,
∴△ABC是直角三角形,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
故答案为:6$\sqrt{3}$.°
点评 此题考查了含30°直角三角形的性质,以及勾股定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
16.函数y=$\sqrt{2-x}$+$\frac{1}{x-1}$中自变量x的取值范围是( )
| A. | x≤2 | B. | x≤2且x≠1 | C. | x<2且x≠1 | D. | x≠1 |
10.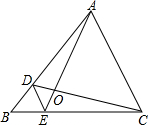 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{16}$ |
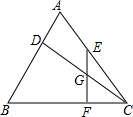 已知:AB=AC,EF⊥BC于F,CD⊥AB,EG=CF,求$\frac{AD}{BD}$的值.
已知:AB=AC,EF⊥BC于F,CD⊥AB,EG=CF,求$\frac{AD}{BD}$的值.
 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为$\frac{π}{3}$.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为$\frac{π}{3}$.