Question

10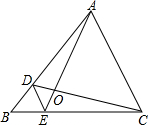．如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S_△BDE：S_△CDE=1：3，则S_△DOE：S_△AOC的值为（　　）

• A． $\frac{1}{3}$
• B． $\frac{1}{4}$
• C． $\frac{1}{9}$
• D． $\frac{1}{16}$

Answer 1

分析 证明BE：EC=1：3，进而证明BE：BC=1：4；证明△DOE∽△AOC，得到$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$，借助相似三角形的性质即可解决问题．

解答 解：∵S_△BDE：S_△CDE=1：3，
∴BE：EC=1：3；
∴BE：BC=1：4；
∵DE∥AC，
∴△DOE∽△AOC，
∴$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$，
∴S_△DOE：S_△AOC=${（\frac{DE}{AC}）}^{2}$=$\frac{1}{16}$，
故选D．

点评 本题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用形似三角形的判定及其性质来分析、判断、推理或解答．