Question

9．在Rt△ABO中，∠AOB=90°，OA=$\frac{4}{3}\sqrt{3}$，OB=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE．
（Ⅰ）如图①，当E点恰好落在线段AB上时，求E点坐标；
（Ⅱ）在（Ⅰ）问的条件下，将△ODE沿x轴的正半轴向右平移得到△O′D′E′，O′E′、D′E′分别交AB于点G、F（如图②）求证OO′=E′F；
（Ⅲ）若点D沿x轴正半轴向右移动，设点D到原点的距离为x，△ODE与△AOB重叠部分的面积为y，请直接写出y与x的函数关系式．

Answer 1

分析 （1）由题意作辅助线，作EH⊥OB于点H，由BO=4，求得OE，然后求出OH，EH，从而得出点E的坐标；
（2）假设存在，由OO′=4-2-DB，而DF=DB，从而得到OO′=EF；
（3）根据题意分三种情况写出解析式即可．

解答 解：（1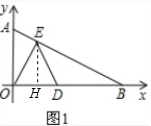）作EH⊥OB于点H，
tan∠ABO=$\frac{OA}{OB}$=$\frac{\frac{4}{3}\sqrt{3}}{4}$=$\frac{\sqrt{3}}{3}$，
∴∠ABO=30°，
∵△OED是等边三角形，
∴∠EOD=60°．
又∵∠ABO=30°，
∴∠OEB=90°．
∵BO=4，
∴OE=$\frac{1}{2}$OB=2．
∵△OEH是直角三角形，且∠OEH=30°
∴OH=1，EH=$\sqrt{3}$．
∴E（1，$\sqrt{3}$）；
（2）∵∠ABO=30°，∠EDO=60°，
∴∠ABO=∠DFB=30°，
∴D′F=D′B．
∴OO′=4-2-D′B=2-D′B=2-D′F=E′D′-FD′=E′F；
（3）当0＜x≤2时，△ODE与△AOB重叠部分的面积为△ODE面积=$\frac{\sqrt{3}}{4}$x²，
当2＜x＜4时，△ODE与△AOB重叠部分的面积为四边形GO′DF面积=-$\frac{\sqrt{3}}{4}$x²+2$\sqrt{3}$x-2$\sqrt{3}$，
当x≥4时，△ODE与△AOB重叠部分的面积为2$\sqrt{3}$．

点评 本题考查的是等边三角形的性质、坐标与图形的关系、锐角三角函数的定义以及二次函数解析式的确定，掌握平移规律、熟记锐角三角函数的定义是解题的关键．