题目内容
8.化简($\frac{m-3}{{m}^{2}+3m}$-$\frac{m-1}{{m}^{2}+6m+9}$)÷$\frac{{m}^{2}-9}{m+3}$,并选择一个合适的数代入求值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把m=1代入计算即可求出值.
解答 解:原式=[$\frac{m-3}{m(m+3)}$-$\frac{m-1}{(m+3)^{2}}$]•$\frac{m+3}{(m+3)(m-3)}$
=$\frac{{m}^{2}-9-{m}^{2}+m}{m(m+3)^{2}}$•$\frac{m+3}{(m+3)(m-3)}$
=$\frac{m-9}{m(m+3)^{2}(m-3)}$,
当m=1时,原式=$\frac{1}{4}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
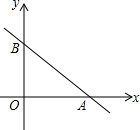
 如图,已知函数y=kx+2与函数y=mx-4的图象交于点A,根据图象可知不等式kx+2<mx-4的解集是x<-3.
如图,已知函数y=kx+2与函数y=mx-4的图象交于点A,根据图象可知不等式kx+2<mx-4的解集是x<-3.
 在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+3的图象与x、y轴分别交于点A、B.
在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+3的图象与x、y轴分别交于点A、B. 已知点P为线段AB上一点,射线PM⊥AB,用直尺和圆规在PM上找一点C,使得PC2=AP•PB.
已知点P为线段AB上一点,射线PM⊥AB,用直尺和圆规在PM上找一点C,使得PC2=AP•PB. 在Rt△ABC中,∠C=90°,AC=4,BC=3,现将延长BC到D,使△ABD为等腰三角形,求等腰△ABD的周长.
在Rt△ABC中,∠C=90°,AC=4,BC=3,现将延长BC到D,使△ABD为等腰三角形,求等腰△ABD的周长.