Question

18．如图，已知AB是⊙O的直径，C、D为⊙O上两点，CG⊥AB于点F，CE⊥AD的延长线于点E，且CE=CF．
（1）求证：CE是⊙O的切线；
（2）若AD=CD=6，连接AG，求△ACG的面积．

Answer 1

分析 （1）连接OC．根据角平分线性质定理的逆定理，得∠CAE=∠CAB．根据OC=OA，得到∠CAB=∠OCA，从而得到∠CAE=∠OCA，根据内错角相等，两条直线平行，得到OC∥AE，从而根据切线的判定证明结论；
（2）根据AD=CD，得到∠DAC=∠DCA=∠CAB，从而DC∥AB，得到四边形AOCD是平行四边形．根据平行四边形的性质，得OC=AD=6，则AB=12．根据∠CAE=∠CAB，得到$\widehat{CD}$=$\widehat{BC}$，则△OCB是等边三角形，根据等边三角形的性质求得CF=3 $\sqrt{3}$，再根据梯形的面积公式进行计算．

解答 解：（1）连接OC．
∵CF⊥AB，CE⊥AD，且CE=CF，
∴∠CAE=∠CAB．
∵OC=OA，
∴∠CAB=∠OCA，
∴∠CAE=∠OCA，
∴OC∥AE，
∴OC⊥CE，
又∵OC是⊙O的半径，
∴CE是⊙O的切线；

（2）∵AD=CD，
∴∠DAC=∠DCA=∠CAB，
∴DC∥AB．
∵∠CAE=∠OCA，
∴OC∥AD，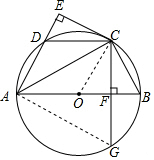
∴四边形AOCD是平行四边形．
∴OC=AD=6，AB=12．
∵∠CAE=∠CAB，
∴$\widehat{CD}$=$\widehat{BC}$，
∴CD=CB=6，
∴△OCB是等边三角形，
∴CF=3∴AF=9，CG=6$\sqrt{3}$，
∴S_△ACG=$\frac{1}{2}$CG•AF=$\frac{1}{2}×$6$\sqrt{3}$×9=27$\sqrt{3}$．

点评 此题综合运用了切线的判定、角平分线性质定理的逆定理、平行线的判定和性质、圆周角定理的推论、等边三角形的判定和性质，是一道综合性较强的题目．