题目内容
1.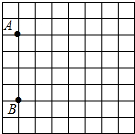 有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,
有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,(1)请通过建立直角坐标系找到图中C点的位置;
(2)请作出三角形ABC关于y轴对称的图形三角形A1B1C1;
(3)请求出三角形ABC的周长和面积.
分析 (1)根据A点坐标可确定原点位置,然后画出平面直角坐标系,然后再标出C的位置;
(2)首先确定A、B、C三点关于y轴对称点的位置,然后连接即可;
(3)利用勾股定理计算出AC、BC的长,然后求周长即可,面积利用AB的长乘以AB上的高,再除以2即可.
解答 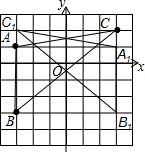 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)AC=$\sqrt{{1}^{2}+{6}^{2}}$=$\sqrt{37}$,BC=$\sqrt{{5}^{2}+{6}^{2}}$=$\sqrt{61}$,
三角形ABC的周长:$\sqrt{37}$+$\sqrt{61}$+4;
面积:$\frac{1}{2}×$4×6=12.
点评 此题主要考查了作图--轴对称变换,以及勾股定理,关键是正确确定原点位置,画出坐标系.

练习册系列答案
相关题目
11.已知一个三角形的两边长分别是4和10,那么它的第三边长可能是下列值中的( )
| A. | 5 | B. | 6 | C. | 11 | D. | 16 |
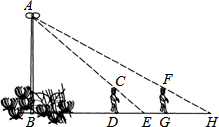 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.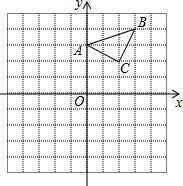 已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
已知:在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)