题目内容
20. 为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?
为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是多少?
分析 首先根据题意确定一次函数与反比例函数的解析式,然后代入y=3确定两个自变量的值,差即为有效时间.
解答 解:设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
将(8,6)代入,得6=8k1,解得k1=$\frac{3}{4}$;
设药物燃烧后y关于x的函数关系式为y=$\frac{k_2}{x}$(k2>0),
将(8,6)代入,得6=$\frac{k_2}{8}$,解得k2=48,
所以药物燃烧时y关于x的函数关系式为y=$\frac{3}{4}x$(0≤x≤8),
药物燃烧后y关于x的函数关系式为y=$\frac{48}{x}$(x>8);
把y=3代入y=$\frac{3}{4}x$,得:x=4,
把y=3代入y=$\frac{48}{x}$,得:x=16.
16-4=12.
故此次消毒的有效时间是12分钟.
点评 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
10.用10米长的铝材制成一个矩形窗框,使它的面积为6平方米,若设它的一条边长为x米,则根据题意可列出的关于x的方程为( )
| A. | x(10÷2+x)=6 | B. | x(10÷2-x)=6 | C. | x(10-x)=6 | D. | x(x-1)=28 |
11.已知一个三角形的两边长分别是4和10,那么它的第三边长可能是下列值中的( )
| A. | 5 | B. | 6 | C. | 11 | D. | 16 |
 如图,现在甲、乙、丙三家公司共建一个污水处理站,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
如图,现在甲、乙、丙三家公司共建一个污水处理站,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)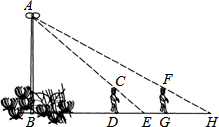 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.