题目内容
19. 如图,∠ABC=∠DCB=90°,且AC=BD.AB与DC相等吗?∠BAC与∠CDB相等吗?为什么?
如图,∠ABC=∠DCB=90°,且AC=BD.AB与DC相等吗?∠BAC与∠CDB相等吗?为什么?
分析 由AC=BD、BC=BC结合勾股定理可得出AB=DC,在△ABC和△DCB中由SSS即可得出△ABC≌△DCB,根据全等三角形的性质可得出∠BAC=∠CDB.
解答 证明:AB=DC,∠BAC=∠CDB.
由勾股定理得:AB=$\sqrt{A{C}^{2}-B{C}^{2}}$,DC=$\sqrt{B{D}^{2}-B{C}^{2}}$,
又∵AC=BD,
∴AB=DC.
在△ABC和△DCB中,$\left\{\begin{array}{l}{AC=BD}\\{BC=BC}\\{AB=DC}\end{array}\right.$,
∴△ABC≌△DCB(SSS),
∴∠BAC=∠CDB.
点评 本题考查了全等三角形的判定与性质,解题的关键是证出△ABC≌△DCB.本题属于基础题,难度不大,解决该类型题目时,可以利用直角三角形全等的判定定理HL来得出结论.

练习册系列答案
相关题目
10.用10米长的铝材制成一个矩形窗框,使它的面积为6平方米,若设它的一条边长为x米,则根据题意可列出的关于x的方程为( )
| A. | x(10÷2+x)=6 | B. | x(10÷2-x)=6 | C. | x(10-x)=6 | D. | x(x-1)=28 |
7.有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2-3(x>0),y=$\frac{2}{x}$(x>0),y=-$\frac{1}{3x}$(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.已知一个三角形的两边长分别是4和10,那么它的第三边长可能是下列值中的( )
| A. | 5 | B. | 6 | C. | 11 | D. | 16 |
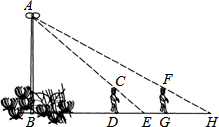 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.